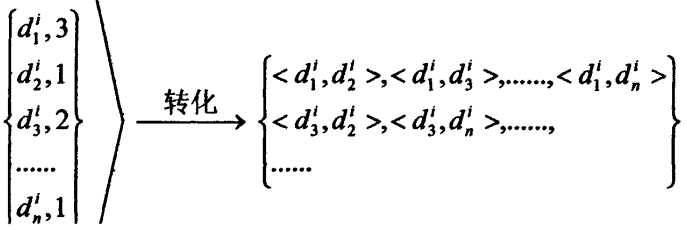Boosting,迭代,即通过迭代多棵树来共同决策。GBDT的核心就在于,每一棵树学的是之前所有树结论和的残差,这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁,但第一棵树的预测年龄是12岁,差了6岁,即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习,如果第二棵树真的能把A分到6岁的叶子节点,那累加两棵树的结论就是A的真实年龄;如果第二棵树的结论是5岁,则A仍然存在1岁的残差,第三棵树里A的年龄就变成1岁,继续学习。
比如年龄预测,假设训练集只有4个人A,B,C,D,他们的年龄分别是14,16,24,26。其中A,B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。若用一棵传统的回归决策树来训练,会得到如图所示结果。
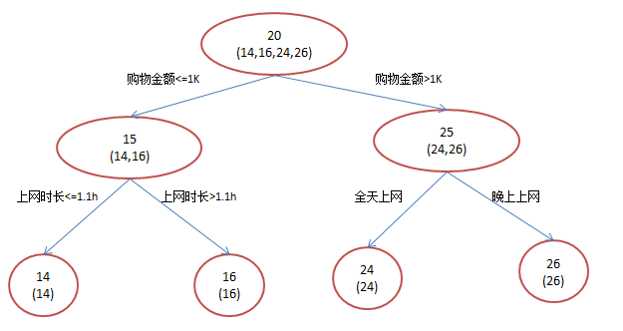
如果使用GBDT来来训练,由于数据太少,我们限定叶子节点做最多有两个,并且限定只学两棵树。
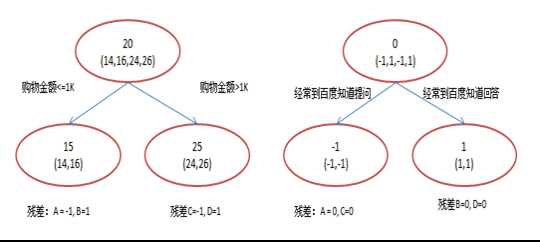
A: 14岁高一学生,购物较少,经常问学长问题;预测年龄A = 15 – 1 = 14
B: 16岁高三学生;购物较少,经常被学弟问问题;预测年龄B = 15 + 1 = 16
C: 24岁应届毕业生;购物较多,经常问师兄问题;预测年龄C = 25 – 1 = 24
D: 26岁工作两年员工;购物较多,经常被师弟问问题;预测年龄D = 25 + 1 = 26
注:图1和图2
最终效果相同,为何还需要GBDT呢?答案是过拟合。过拟合是指为了让训练集精度更高,学到了很多“仅在训练集上成立的规律”,导致换一个数据集当前规律就不适用了。只要允许一棵树的叶子节点足够多,训练集总是能训练到100%准确率的。在训练精度和实际精度(或测试精度)之间,后者才是我们想要真正得到的。
2.4 Shrinkage
Shrinkage(缩减)的思想认为:每次走一小步逐渐逼近结果,要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树,它认为每棵树只学到了结果的一小部分,累加的时候只累加一小部分,通过多学几棵树弥补不足。
假设yi表示第i棵树上y的预测值,y(1~i)表示前i棵树y的综合预测值。
y(i+1)= f(残差(y(1~i)))
其中,残差(y(1~i))=y真实值 - y(1~i)
y_(1~i)= SUM(y_1,…, y_i)
引入Shrinkage后,y(1~i) = y(1~i-1)+step *yi
step可以认为是学习速度,越小表示学习越慢,越大表示学习越快。step一般都比较小,导致各个树的残差是渐变的而不是陡变的。
三. GBDT适用范围
机器学习可以解决很多问题,其中最为重要的两个是 回归与分类。GBDT可用于回归问题,相对logistic
regression仅能用于线性回归,GBDT能用于线性回归和非线性回归,GBDT的适用面非常广。GBDT也可用于二分类问题(设定阈值,大于阈值为正例,反之为负例)。
四. 搜索引擎排序应用RankNet
RankNet是基于样本对级别(机器学习按照误差函数的设计分为3种:点方式、对方式、列表方式)方法的一种典型的网页排序算法,是利用梯度下降的原理,基于神经网络来进行模型的构造和应用的。
就像所有的机器学习一样,搜索排序的学习也需要训练集,RankNet一般是用人工标注实现,即对每一个文档给定一个分值(1,2,3,4),分值越高表示越相关,越应该排到前面。然而这些绝对的分值本身意义不大,例如很难说1分和2分文档的相关程度差异是1分和3分文档相关程度差距的一半。相关度是一个很主观的评判,人工无法做到这种定量标注,这种标准也无法制定。但人工容易做到的是“A和B与查询词都很相关,但文档A比文档B更相关,所以A比B的分高”。
利用RankNet进行网页排序,首先对训练样本进行转化。
利用神经网络进行训练。假设在训练样本中对于查询q存在<xi, xj>文档序列对,需要计算2个概率值P1和P2。
P1这个概率是由神经网络模型计算出来的,函数如下
P2=e^(o_ij
)/(1+e^(o_ij ) )
其中,对于文档xi,
xj,神经网络模型f对其打分分别为o_i=f(xi), o_j=f(xj),并记o_ij=o_i-o_j。
模型f:R^d→R R^d是文档的特征空间,R是实数。
对于概率P2,它表示真实存在的概率,标记了文档x_i和x_j的真实优先关系。根据人工对文档的打分,若文档xi
与查询q的相关度大于文档xj,则记P2=1;反之记P2=0;若文档xi
与查询q的相关度等于文档xj,则记P2=0.5。神经网络模型的目的是使计算出来的P1符合P2。
定义误差函数,使用交叉熵来计算误差,文档x_i 与x_j的交叉熵计算公式为:
C_ij=-P2 log?〖P1 〗-(1-P2 ) log?〖P1
〗
= -P2 o_ij + log?〖(1+e^(o_ij
))〗
对于整个模型的误差,只需要将所有文档序对的误差进行求和就可以得到。得到误差后,利用梯度下降的原理,计算出其梯度。然后利用BP型神经网络,就可以对其样本进行训练(每次对两个样本的输入进行一次神经网络的权重调整)。最后,每个样本通过Shrinkage累加都会得到一个最终分数,直接按分数从大到小对样本进行排序。