SG函数模板

首先定义mex(minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。

对于一个给定的有向无环图，定义关于图的每个顶点的Sprague-Grundy函数g如下：g(x)=mex{ g(y) | y是x的后继 },这里的g（x）即sg[x]

例如：取石子问题，有1堆n个的石子，每次只能取{1，3,4}个石子，先取完石子者胜利，那么各个数的SG值为多少？

sg[0]=0，f[]={1,3,4},  //我们可以将 f[] , 从小到大排序

x=1时，可以取走1-f{1}个石子，剩余{0}个，mex{sg[0]}={0}，故sg[1]=1;

x=2时，可以取走2-f{1}个石子，剩余{1}个，mex{sg[1]}={1}，故sg[2]=0；

x=3时，可以取走3-f{1,3}个石子，剩余{2,0}个，mex{sg[2],sg[0]}={0,0}，故sg[3]=1;

x=4时，可以取走4-f{1,3,4}个石子，剩余{3,1,0}个，mex{sg[3],sg[1],sg[0]}={1,1,0},故sg[4]=2;

x=5时，可以取走5-f{1,3,4}个石子，剩余{4,2,1}个，mex{sg[4],sg[2],sg[1]}={2,0,1},故sg[5]=3；

注意：

f[]需要从小到大排序

1.可选步数为1~m的连续整数，直接取模即可，SG(x) = x % (m+1);

2.可选步数为任意步，SG(x) = x;   ， Nim问题

3.可选步数为一系列不连续的数，用GetSG()计算

模板1如下：

// SG打表， 利用动态规划

int f[N],sg[N];
void getSG(int x)   
{
    sg[0]=0;
    for(int i=1; i<=x ; i++)  // 这个x 是所有要用到的x 的最大值
    {
        set<int>S;  // 集合中无重复的元素， 且元素是按从小到大排序
        for(int j=0 ; f[j]<= i; j++)         // f[]数组 的下标是 从0开始的
            S.insert(sg[i-f[j]]);
        int g=0;
        while(S.count(g) != 0) g++;
        sg[i] = g;
    }
}

模板2如下：（dfs）

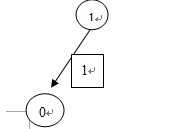 sg[1] =mex{sg[0]} = mex{0}  sg[1] =1

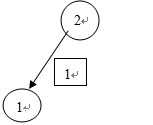sg[2] = mex{sg[1]} =  mex{1}  sg[2] = 0

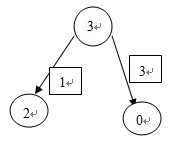sg[3] = mex{sg[2], sg[0]} = mex{0, 0} = 1

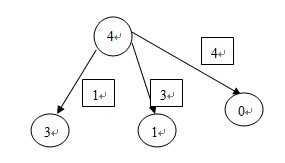sg[4] = mex{sg[3], sg[1], sg[0]} = mex{1, 1, 0}  sg[4] = 2

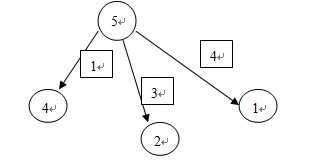sg[5] =  mex{sg[4], sg[2], sg[1]} = mex{2, 0, 1}  sg[5] = 3

代码如下：

//注意 f数组要按从小到大排序
//SG函数要初始化为-1 对于每个集合只需初始化1遍
//n是集合f的大小 f[i]是定义的特殊取法规则的数组

int f[N_f],vis[N_f];
int sg[N_x],n;
int SG_dfs(int x)
{
    int i;
    if(sg[x]!=-1)
        return sg[x];
    memset(vis,0,sizeof(vis));
    for(i=0;i<n;i++)  // n是集合f[]的大小
    {
        if(x>=f[i])
        {
            SG_dfs(x-f[i]);
            vis[sg[x-f[i]]]=1;
        }
    }
    int e;
    for(i=0;;i++)
        if(!vis[i])
        {
            e=i;
            break;
        }
    return sg[x]=e;
}

SG函数模板,布布扣,bubuko.com

SG函数模板

原文：http://www.cnblogs.com/zn505119020/p/3608051.html