无监督学习（unsurpervised learning）是深度学习的基础，也是大数据时代科学家们用来处理数据挖掘的主要工具。个人理解的话就是数据太多，而人们不可能给每个数据样本加标签吧，所以才有了无监督学习。当然用的最多的是用无监督学习算法训练参数，然后用一部分加了标签的数据测试。这种方法叫半监督学习（semi-unsurpervised）。最近看的几个深度学习算法是：稀疏自编码(sparse auto-encoder)、稀疏限制玻尔兹曼机器（sparse RBM）、K-means 聚类和高斯混合模型。根据论文An Analysis of Single-Layer Networks in Unsupervised Feature Learning的实验结果，K-means聚类算法是准确率最高，而且不需要超参数（hyper-parameter）。
稀疏自编码（sparse auto-encoder）
提到自编码，就必须了解BP神经网络。而稀疏自编码是在自编码基础上加入了对隐藏单元活性（activition）的限制：即稀疏性参数ρ，通常是一个接近于0的较小值（比如ρ=0.05）。如果机器学习的基础比较薄弱的话，建议先看Andrew Ng 老师讲授的《机器学习》。
BP神经网络，是使用前向传播（forward propagation）、后向传播（backward propagation）来训练参数。这里给出前向传播和后向传播的公式，具体细节见参考资料：
前向传播（向量表示法）：
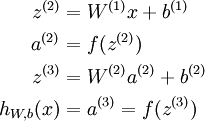
其中，f(x)称为激活函数（activation function）.可以或者激活函数
sigmoid函数:
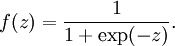取值范围[0,1].它的导数就是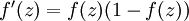
双曲正切函数:
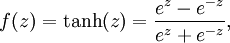取值范围[-1,1]。它的导数是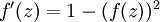 
（激活函数的导数在后向传播中会经常用到）
后向传播：
前向传播中，需要用到的参数W和b，是我们要训练的参数。我们可以利用批量梯度下降的方法求得（这部分需要熟悉机器学习中梯度下降部分）。给定一个包含m个样例的数据集，我们可以定义整体代价函数为：
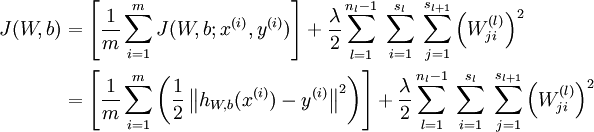
其中，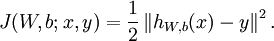
第一项中的 
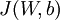是一个均方差项；第二项则是一个正规化项，其目的是减少权值的幅度，防止过度拟合。
于是就有了梯度下降法中每一次迭代对W和b的更新：
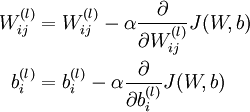
其中α是学习速率。而关键步骤则是计算偏导数~这个，就是我们要讲的后向传播算法了。
整体代价函数的的偏导数：
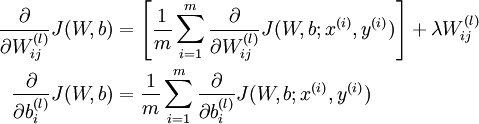
现在对其分析可以知道::
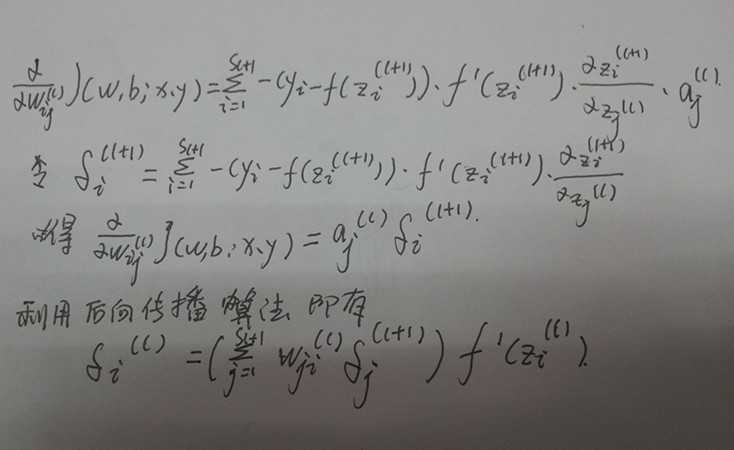
于是，后向传播算法就是在说明针对第 
层的每一个节点 
，我们计算出其“残差”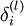
。
天才的科学家们提出了如下的计算过程：
直到输出层 
的激活值。 2.对于第 
层（输出层）的每个输出单元 ，我们根据以下公式计算残差：
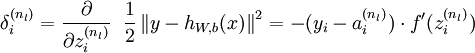
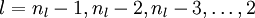的各个层，第 层的第 个节点的残差计算方法如下：
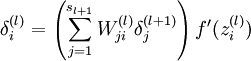
4.计算我们需要的偏导数，计算方法如下：
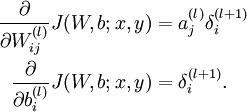
最后，我们将对梯度下降算法做个全面总结。在下面的伪代码中，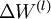
是一个与矩阵 
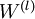维度相同的矩阵，
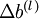是一个与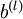 
维度相同的向量。注意这里“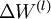”是一个矩阵，而不是“
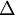与 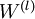相乘”。下面，我们实现批量梯度下降法中的一次迭代：
，令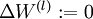 
, 
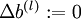（设置为全零矩阵或全零向量）
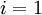到 
，
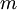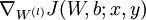和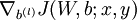 
。
。
。
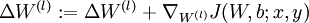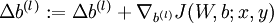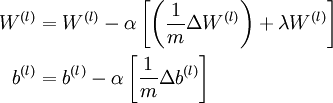
於乎~就这样了。。。
下面就好办了，对于自编码，无非就是尝试学习一个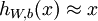 
的函数。而稀疏自编码则是给隐藏神经元加入稀疏性限制。
呐:
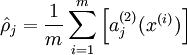
表示隐藏神经元j的平均活跃度，而限制则是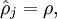
是稀疏性参数，通常是一个接近于0的较小的值（比如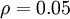 
）。
于是有了惩罚因子：
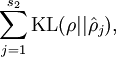等于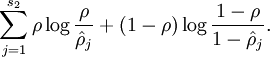
这是相对熵的公式表示形式，意义在于当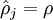 
时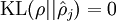 
。相对熵的三条结论：
1.对于两个完全相同的函数，它们的相对熵等于0.
2.相对熵越大，两个函数差异越大；反之，相对熵越小，差异越小。
3.对于概率分布或者概率密度分布，如果取值均大于零，相对熵可以度量两个随机分布的差异性。
（引用吴军老师《数学之美》中的结论）。
所以，稀疏自编码的总体代价函数就是：
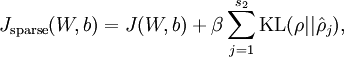
而实际与后向传播不同的地方就是：
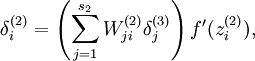
现在我们将其换成
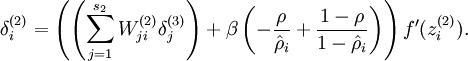
参考资料：
1，斯坦福大学关于深度学习的网站（其实你只要看这个，稀疏自编码你就明白了，我的基本算是copy这的）
http://deeplearning.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B
2，Andrew Ng老师讲解的《机器学习课程》
http://openclassroom.stanford.edu/MainFolder/CoursePage.php?course=MachineLearning
无监督学习一些算法的简要概括（一）-稀疏自编码,布布扣,bubuko.com
原文：http://www.cnblogs.com/cherler/p/3604720.html