这是一个家族谱:
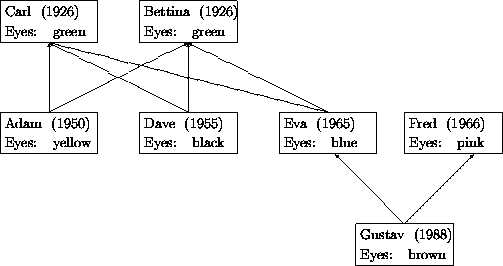
;child
(define-struct child (father mother name date eyes))
#lang racket ;child (define-struct child (father mother name date eyes)) ;; Oldest Generation: (define Carl (make-child empty empty ‘Carl 1926 ‘green)) (define Bettina (make-child empty empty ‘Bettina 1926 ‘green)) ;; Middle Generation: (define Adam (make-child Carl Bettina ‘Adam 1950 ‘yellow)) (define Dave (make-child Carl Bettina ‘Dave 1955 ‘black)) (define Eva (make-child Carl Bettina ‘Eva 1965 ‘blue)) (define Fred (make-child empty empty ‘Fred 1966 ‘pink)) ;; Youngest Generation: (define Gustav (make-child Fred Eva ‘Gustav 1988 ‘brown)) ;判断a-ftree是否包含一个child结构体,其eyes为blue (define (blue-eyed-ancestor? a-ftree) (cond [(empty? a-ftree) false] [else (cond [(symbol=? (child-eyes a-ftree) ‘blue) true] [(blue-eyed-ancestor? (child-father a-ftree) ) true] [(blue-eyed-ancestor? (child-mother a-ftree)) true] [else false] ) ])) (blue-eyed-ancestor? Gustav)
;求家谱树种人数 (define (count-persons a-ftree) (cond [(empty? a-ftree) 0] [else (+ 1 (+ (count-persons (child-father a-ftree)) (count-persons (child-mother a-ftree))) )])) (count-persons Carl) (count-persons Adam)
x题目:
读入一个家谱树节点和当前年份,返回所有人的平均年龄:
(define (sum-of-ages a-ftree current-year) (cond [(empty? a-ftree) 0] [else (+ (- current-year (child-date a-ftree) ) (+ (sum-of-ages (child-father a-ftree) current-year) (sum-of-ages (child-mother a-ftree) current-year) ) )]) ) (define (average-age a-ftree current-year) (/ (sum-of-ages a-ftree current-year) (count-persons a-ftree)))
题目:
Exercise 14.1.5. Develop the function eye-colors, which consumes a
family tree node and produces a list of all eye colors in the tree. An eye color may occur more than once in the
list.
Hint: Use the Scheme operation append, which consumes two lists and produces the
concatenation of the two lists. For example:
(append (list ‘a ‘b ‘c) (list ‘d ‘e)) = (list ‘a ‘b ‘c ‘d ‘e)
We discuss the development of functions like append in section 17. ![]() Solution
Solution
(define (eye-colors a-ftree) (cond [(empty? a-ftree) empty] [else (cons (child-eyes a-ftree) (append (eye-colors (child-father a-ftree)) (eye-colors (child-mother a-ftree)) ))] ))
二叉树:
binary tree Bt是这样2者之一:
1.false
2.(make-node soc pn lft rgt) 其中soc是数,pn是符号,lft和rgt是BT。
这里选用false来表示缺乏信息,这一点是任意的,事实上,恩也可以选用empty,不过,我们更熟悉false,而且比起其他东西,他更好用。
函数bt-contains? 读入一个数和一颗树,判断这个数是否在树中出现:
14.1.6 | Problem Statement | Table of Contents | 14.2.2 ;; Language: Beginning Student ; 11 ‘Bobby ; \ ; ; 12 ‘Luke ; 11 ‘Bobby ; / ; / ; 24 ‘Luke ; 11 ‘Bobby ; / ; / ; 24 ‘Luke 5 ‘Paul #| A BT is either 1. false; or 2. (make-node soc pn lft rgt) where soc is a number, pn is a symbol, and lft and rgt are BTs. |# (define-struct node (ssn name left right)) (define bt1 (make-node 11 ‘Bobby false (make-node 12 ‘Luke false false))) (define bt2 (make-node 11 ‘Bobby (make-node 12 ‘Luke false false) false)) (define bt3 (make-node 11 ‘Bobby (make-node 12 ‘Luke false false) (make-node 5 ‘Paul false false))) ;; bt-contains?: number BT -> boolean ;; consumes a number and binary-tree and determines if a-bt contains n (define (bt-contains? n a-bt) (cond [(boolean? a-bt) false] [else (or (= n (node-ssn a-bt)) (bt-contains? n (node-left a-bt)) (bt-contains? n (node-right a-bt)))])) (equal? (bt-contains? 11 bt1) true) (equal? (bt-contains? 5 bt3) true) (equal? (bt-contains? 9 bt3) false) (equal? (bt-contains? 12 bt2) true) (equal? (bt-contains? 5 bt2) false) (equal? (bt-contains? 12 bt3) true)
开发函数search-bt,读入一个数n和BT,如果这棵树包含一个node结构体,其soc字段为n,函数就返回这个节点的pn字段的值,否则,函数返回false:
;; search-bt : number binary-tree -> false or ;; returns true if a-n is in a-bt, and false if not. (define (search-bt a-n a-bt) (cond [(boolean? a-bt) #f] [else (cond [(= (node-ssn a-bt) a-n) (node-name a-bt)] [(boolean? (search-bt a-n (node-left a-bt))) (search-bt a-n (node-right a-bt))] [else (search-bt a-n (node-left a-bt))])]))
这里我们用boolean?检查search-bt是否成功作用于某一科子树。(回溯思想)。
二叉搜索树:BST
A binary-search-tree (short: BST) is a
BT:
falseis always aBST;
(make-node soc pn lft rgt)is aBSTif
lftandrgtareBSTs,all
ssnnumbers inlftare smaller thansoc, andall
ssnnumbers inrgtare larger thansoc.
The second and third conditions are different from what we have seen in
previous data definitions. They place an additional and unusual burden on the
construction BSTs. We must inspect all numbers in these trees
and ensure that they are smaller (or larger) than soc.
二叉树中序变量:
;; DEFINITION: (define (inorder abt) (cond ((boolean? abt) empty) ((node? abt) (append (inorder (node-left abt)) (cons (node-name abt) (inorder (node-right abt)))))))
二叉搜索树搜索:
;; search-bst : number binary-tree -> false or ;; returns true if a-n is in a-bt, and false if not. (define (search-bt a-n a-bt) (cond [(boolean? a-bt) #f] [else (cond [(= (node-ssn a-bt) a-n) (node-name a-bt)] [(< (node-ssn a-bt) a-n) (search-bt a-n (node-right a-bt))] [(> (node-ssn a-bt) a-n) (search-bt a-n (node-left a-bt))])]))
插入;
14.2.4 | Problem Statement | Table of Contents | 14.2.6 ; DATA DEFINITIONS (define-struct node (ssn name left right)) ; A binary tree is either ; 1. false or ; 2. (make-node soc pn lft rgt) ; where soc is a number, pn is a symbol, and lft and rgt are binary ; trees. ;; EXAMPLES ; (create-bst false 6 ‘b) => (make-node 6 ‘b false false) ; ; (create-bst (make-node 4 ‘a false false) 5 ‘a) ; => ; (make-bst 4 ‘a false (make-bst 5 ‘a false false)) ; ; (create-bst (make-node 4 ‘a false false) 3 ‘g) ; => ; (make-node 4 ‘a (make-node 3 ‘g false false) false) ; ; (create-bst (make-node 4 ‘a (make-node 2 ‘a false false) false) 3 ‘g) ; => ; (make-node 4 ‘a (make-node 2 ‘a false (make-node 3 ‘g))) ;; TEMPLATE: ;(define (bst-fun abt) ; (cond ; ((boolean? abt) ...) ; ((node? abt) ; ... (node-ssn abt) ... (node-name abt) ... ; ... (bst-fun (node-left abt)) ... (bst-fun (node-right abt)) ... ))) ;; CONTRACT/HEADER/PURPOSE: ;; create-bst : binary-tree number symbol -> binary-tree ;; to create a binary search tree with the same values as the input tree ;; and also the given number associated with the given name (define (create-bst bst n s) (cond [(eq? bst false) (make-node n s false false)] [else (cond [(< n (node-ssn bst)) (make-node (node-ssn bst) (node-name bst) (create-bst (node-left bst) n s) (node-right bst))] [(> n (node-ssn bst)) (make-node (node-ssn bst) (node-name bst) (node-left bst) (create-bst (node-right bst) n s))] [else (error ‘create-bst "Number already in BST")])])) (equal? (create-bst false 6 ‘b) (make-node 6 ‘b false false)) (equal? (create-bst (make-node 4 ‘a false false) 5 ‘a) (make-node 4 ‘a false (make-node 5 ‘a false false))) (equal? (create-bst (make-node 4 ‘a false false) 3 ‘g) (make-node 4 ‘a (make-node 3 ‘g false false) false)) (equal? (create-bst (make-node 4 ‘a (make-node 2 ‘a false false) false) 3 ‘g) (make-node 4 ‘a (make-node 2 ‘a false (make-node 3 ‘g false false)) false))
感觉这个程序有点奇怪, 但仔细相同时合理的。没有多余的创建node。
开发函数,读入一个由数和名字组成的表,反复调用create-bst,返回一个bst。
; create-bst-from-list : list-of-numbers-and-symbols -> binary-tree ; to produce a binary tree with all the numbers in the input list ; associated with their corresponding symbols (define (create-bst-from-list lons) (cond· [(empty? lons) false] [else (create-bst (create-bst-from-list (rest lons)) (first (first lons)) (second (first lons)))]))
(equal? (create-bst-from-list ‘((1 a) (18 b) (2 g))) (make-node 2 ‘g (make-node 1 ‘a false false) (make-node 18 ‘b false false)))
为true。
表中的表:
A Web-page (short: WP) is either
empty;
(cons s wp)
where s is a symbol
and wp is a Web page; or
(cons ewp wp)
where both ewp and wp are Web pages.
This data definition differs from that of a list of symbols in that it
has three clauses instead of two and that it has three self-references instead
of one. Of these self-references,
the one at the beginning of a constructed
list is the most unusual. We refer to such Web pages
as immediately embedded Web
pages.
开发函数size,读入一个网页,返回其自身以及所有嵌入网页所包含的单词数。
Let‘s develop the function size, which consumes a Web page and produces the
number of words that it and all of its embedded pages contain:
;;size : WP -> number;; to count the number of symbols that occur ina-wp(define (size a-wp) ...)
The two Web pages above suggest two good examples, but they are too complex. Here are three examples, one per subclass of data:
(= (size empty) 0)
(= (size (cons ‘One empty)) 1)
(= (size (cons (cons ‘One empty) empty)) 1)
开开发size函数,我们可以按照设计诀窍,数据定义说明我们需要3个cond子句,一个子句处理empty页,一个子句处理由符号开始的页,另一个子句处理由嵌入的网页开始的页。虽然第一个测试empty的条件我们已经很熟悉了,但是第2个和第3个条件需要我们进一步检查,因为在数据定于中,这2个子句都使用了cons,所以简单地使用cons?并不能区分这2种数据形式。
如果网页不是empty,那么他必然是cons结构,后两种数据形式之间的特征是表中的第一个元素,换句话说,第二个条件必须使用一个测试a-wp的第一个元素的谓词:
;求网页单词数 (define (size a-wp) (cond [(empty? a-wp) 0] [(symbol? (first a-wp)) (+ 1 (size (rest a-wp)))] [else (+ (size (first a-wp)) (size (rest a-wp)))] ) ) (size ‘(a b c))
注意使用
(size ‘(1 2 3)) 报错:
first: contract violation
expected: (and/c list? (not/c empty?))
given: 1
为什么会报错?
(first (cons 1 2))
. . first: contract violation
expected: (and/c
list? (not/c empty?))
given: ‘(1 . 2)
(first (list 1 2)
正确输出1.
(first lst) The same as (car lst), but only for lists (that are not empty).
求网页深度:
只包含符号的深度为0,包含某个直接嵌入页的深度加1.
;; Language: Intermediate Student ;; depth: web-page -> number ;; computes the depth of embedded web-pages (define (depth a-wp) (cond [(empty? a-wp) 0] [(symbol? (first a-wp)) (depth (rest a-wp))] [else (max (+ (depth (first a-wp)) 1) (depth (rest a-wp)))])) ;;; tests (check-expect (depth ‘()) 0) (check-expect (depth ‘(a)) 0) (check-expect (depth ‘(())) 1) (check-expect (depth ‘(a b c)) 0) (check-expect (depth ‘(a (b (c (d))) e (f (g)) h)) 3)
对这个有点不解:
(max (+ (depth (first a-wp)) 1) (depth (rest a-wp)))]))
这么理解,list的后面一定为empty。
《how to design programs》14章 再论自引用数据,布布扣,bubuko.com
《how to design programs》14章 再论自引用数据
原文:http://www.cnblogs.com/youxin/p/3599397.html