先序中序后序

二叉树的遍历方法有先序中序后序三种方法，先以下图为例解释三种遍历顺序：

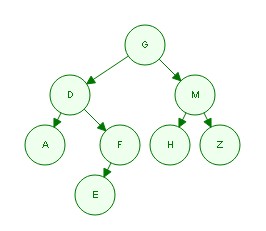
所谓的先后中都是以父节点为中心出发的，即

先序为：父节点、左子节点、右子节点；(父节点第一个)

中序为：左子节点、父节点、右子节点；（父节点放中间，第二个）

后序为：左子节点、右子节点、父节点；（父节点最后一个）

以上图为例，

先序遍历顺序为：GDAFEMHZ

中序遍历顺序为：ADEFGHMZ

后序遍历顺序为：AEFDHZMG

在此三种遍历顺序的基础上，已知中序和另外一种遍历即可获取第三种遍历顺序，即中序遍历+任意一种遍历顺序确定一棵二叉树。

已知先序中序

先序遍历第一个总是根节点，中序遍历根节点总在左子树和右子树中间。因此，先序的第一个数就是根节点，然后在中序中找到该根节点，左边为左子树，右边为右子树。接着再分别拿左子树右子树来判断后续，原理同上。

找到一个算法：

 #include <iostream>  
 #include <fstream>  
 #include <string>  
 
 struct TreeNode
 {
   struct TreeNode* left;
   struct TreeNode* right;
   char  elem;
 };
 
 void BinaryTreeFromOrderings(char* inorder, char* preorder, int length)
 {
   if(length == 0)
     {
       //cout<<"invalid length";
       return;
     }
   TreeNode* node = new TreeNode;//Noice that [new] should be written out.
   node->elem = *preorder;
   int rootIndex = 0;
   for(;rootIndex < length; rootIndex++)
     {
       if(inorder[rootIndex] == *preorder)
       break;
     }
   //Left
   BinaryTreeFromOrderings(inorder, preorder +1, rootIndex);
   //Right
   BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));
   cout<<node->elem<<endl;
   return;
 }
 
 
 int main(int argc, char* argv[])
 {
     char* pr="GDAFEMHZ";
     char* in="ADEFGHMZ";
   
     BinaryTreeFromOrderings(in, pr, 8);
     printf("\n");
     return 0;
 }

已知后序中序

后序遍历最后一个数总是根节点，中序遍历根节点总在左子树和右子树中间。因此，后序的最后一个数就是根节点，然后在中序中找到该数，左边为左子树，右边为右子树。接着再分别拿左子树和右子树按上述方法遍历。

算法如下：

#include <iostream>
#include <fstream>
#include <string>

struct TreeNode
{
    struct TreeNode* left;
    struct TreeNode* right;
    char  elem;
};


TreeNode* BinaryTreeFromOrderings(char* inorder, char* aftorder, int length)
{
    if(length == 0)
    {
        return NULL;
    }
    TreeNode* node = new TreeNode;//Noice that [new] should be written out.
    node->elem = *(aftorder+length-1);
    std::cout<<node->elem<<std::endl;
    int rootIndex = 0;
    for(;rootIndex < length; rootIndex++)//a variation of the loop
    {
        if(inorder[rootIndex] ==  *(aftorder+length-1))
            break;
    }
    node->left = BinaryTreeFromOrderings(inorder, aftorder , rootIndex);
    node->right = BinaryTreeFromOrderings(inorder + rootIndex + 1, aftorder + rootIndex , length - (rootIndex + 1));
    
    return node;
}

int main(int argc, char** argv)
{
    char* af="AEFDHZMG";    
    char* in="ADEFGHMZ"; 
    BinaryTreeFromOrderings(in, af, 8); 
    printf("\n");
    return 0;
}

注意，已知先序和后序不能唯一确定该二叉树，即不能求出中序遍历顺序。

先序中序后序,布布扣,bubuko.com

先序中序后序

原文：http://blog.csdn.net/fengzhongzhishenfu/article/details/24261225