这个题目 转化为背包的时候 可以看到 物品价值 背包容量 都有 但是没有物品的体积 我们要求的是骑士最大能花的钱数,由于缺少物品的体积 我们可以这样思考,骑士要的钞票面额 就是背包大小 骑士向背包里装物品 物品价值不能超过背包的体积 这时 物品的最大价值是多少。因此我们可以把物品的体积看成物品的价值 ,这时 背包恰好不能再放入物品的状态下 既是物品价值最大的情况 也就是骑士花的钱最多的情况。因为物品价值=物品体积 所以 dp[N]不会超过N
状态转移方程:
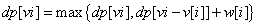
题目及AC代码如下
Time Limit: 2000/1000 MS
(Java/Others) Memory Limit: 65536/32768 K
(Java/Others)
Total Submission(s): 9829 Accepted
Submission(s): 4950
1 #include<stdio.h> 2 #include<string.h> 3 const int max_n=20000; 4 int max(int a,int b) 5 { 6 return a>b?a:b; 7 } 8 int main() 9 { 10 int w[3]={150,200,350}; 11 int v[3]={150,200,350}; 12 int dp[max_n],N; 13 int T; 14 scanf("%d",&T); 15 while(T--) 16 { 17 scanf("%d",&N); 18 memset(dp,0,sizeof(dp)); 19 for(int i=0;i<3;i++) 20 { 21 for(int vi=v[i];vi<=N;vi++) 22 { 23 dp[vi]=max(dp[vi],dp[vi-v[i]]+w[i]); 24 } 25 } 26 printf("%d\n",N-dp[N]); 27 28 } 29 return 0; 30 }
HDU 1248 寒冰王座 完全背包 水题,布布扣,bubuko.com
原文:http://www.cnblogs.com/VOID-133/p/3632692.html