图解hdu5301Buildings

这个题就是给出一个大矩形n*m，其中有个1*1的小格子不能被占用，然后要你用很多小矩形去填满，问小矩形的最小最大面积是多少。

显然小矩形必然是1*x的最好，毕竟i*x，若i>1则还是可以拆成很多1*x。
显然若没有那个被占用的格子，那么答案就是min(n,m)+1>>1。
当考虑这个格子的时候，我们把矩形调整下，保证n<m，然后就很显然，除了被格子占用的那一列j，其他的列k，无论k<j还是k>j必然至少有一个还是用（min(n,m)+1>>1）*1的矩形去竖着填最好，那么考虑只有一个被这种方案填了，那么另一个肯定要用这种方案或者考虑横着填。这两种情况画出来就是这样：

上面的图，同一种颜色代表由同样的1*x的小矩形组成的部分，第一张图的左边是横着插，第二张图右边都是竖着插。

于是就可以很显然的推出式子。另外再单独考虑n=m，且都是奇数，切被占格子在正中间的情况即可。

#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<iostream>
#include<algorithm>
#include<bitset>
#include<climits>
#include<list>
#include<iomanip>
#include<stack>
#include<set>
using namespace std;
int a[10];
int main()
{
	int n,m,x,y;
	while(cin>>n>>m>>x>>y)
	{
		if(n==m&&(n&1)&&x==n+1>>1&&y==x)
		{
			cout<<(n+1>>1)-1<<endl;
			continue;
		}
		if(n>m)
		{
			swap(n,m);
			swap(x,y);
		}
		a[0]=x-1;
		a[1]=n-x;
		a[2]=y;
		a[3]=m-y+1;
		a[4]=n+1>>1;
		int ans=max(a[4],min(max(a[0],a[1]),min(a[2],a[3])));
		cout<<ans<<endl;
	}
}

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 1237    Accepted Submission(s): 335

Your current task is to make a ground plan for a residential building located in HZXJHS. So you must determine a way to split the floor building with walls to make apartments in the shape of a rectangle. Each built wall must be paralled to the building‘s sides.

The floor is represented in the ground plan as a large rectangle with dimensions n×m, where each apartment is a smaller rectangle with dimensions a×b located inside. For each apartment, its dimensions can be different from each other. The number a and b must be integers.

Additionally, the apartments must completely cover the floor without one 1×1 square located on (x,y). The apartments must not intersect, but they can touch.

For this example, this is a sample of n=2,m=3,x=2,y=2.



To prevent darkness indoors, the apartments must have windows. Therefore, each apartment must share its at least one side with the edge of the rectangle representing the floor so it is possible to place a window.

Your boss XXY wants to minimize the maximum areas of all apartments, now it‘s your turn to tell him the answer.

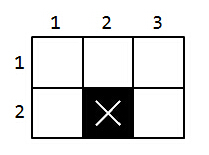
2 3 2 2
3 3 1 1

1
2

Hint
Case 1 :

You can split the floor into five 1×1 apartments. The answer is 1.

Case 2:

You can split the floor into three 2×1 apartments and two 1×1 apartments. The answer is 2.


If you want to split the floor into eight 1×1 apartments, it will be unacceptable because the apartment located on (2,2) can‘t have windows.
 

图解hdu5301Buildings

原文：http://blog.csdn.net/stl112514/article/details/47043967