本文纯属原创,转载请注明出处。谢谢。
题目传送门:http://poj.org/problem?id=1449
| Time Limit: 1000MS | Memory Limit: 10000K | |
Description

Input
Output
Sample Input
2 wfbtiznuvcqejpokshxgmadyrl hmrgnqpkjcaivwluebfzsyxtdo druahlbfzvgmwckxpiqysontje owtvskypjifmluahrqecndbzgx ?bcdefghijklmnopqrstuvwxyz aaaa manyorganizationsrelyoncom??ters grsuztldsznkwnerdpfbovvqnobkyiqn oqzunvhtxwryfebicmjpklsgda zupogrskynxtwdfqvbliejcmha kzvlyjuodmscewxtfbphriqgna gbcnylaztwkfmdspqvoiurjxeh rfyhkxbuvplgtqmdiewjosznca dmeo ??? ave
Sample Output
Scenario #1: manyorganizationsrelyoncomputers Scenario #2: acm
这道题题目长的我这种英语不好的愣是看了半天。
这是2001年XX欧现场赛的题,题目又臭又长,关键其实就是一个十足的水题,关键是网上暂时还找不到这个题的题解,只有赵端阳写的《acm国际大学生程序设计竞赛题解1》里面有提到这道题,但是讲解不够详细,没有解释这个机器的工作原理,所以看了一天多才看懂,然后就毅然决定写一篇来好好解释一下。
大意是这样的:(算了我还是先解释一下这个机器)
首先Enigma作为德国二战时期御用的加密解密器,这个题完完全全地还原了这台天才之作的结构。
它由一个置换盘,3个置换转子盘,和一个反射转子盘组成。
首先是置换盘是一个简单的替换加密器,正向通过时A替换成X,反向通过时X就替换成A,它是固定的,也是最基础最简单的加密方法。《福尔摩斯探案集》里面《跳舞的小人》一节就是用的这个方法,简单地来说就是用26个新的符号替换原来的26个字母,虽然这里替换的26个符号也是取自26个字母,但是它们替换之后就不代表原来的意思了。而反过来就是将26个字符对应替换回原来的字母。
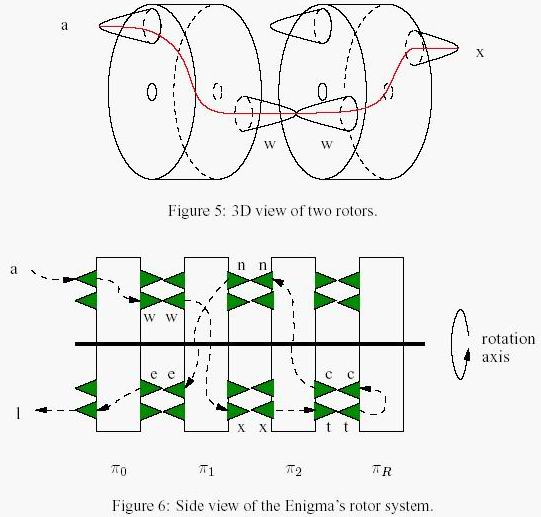
接着最难理解的是3个置换转子,这也是这个机器的精髓。昨天没有看到电路图的时候我一直在想怎么实现的,后来看了一眼电路图瞬间明白了。下面放图。
这是一个置换转子盘的工作原理图。
我们可以看到,无论是明文(左盘)还是密文(右盘),都是按顺序排列而且不变的,变的是中间的转子电路圈。而我们可以看到,置换电路圈的电路是不变的,那么如果一开始A连到D,那么代表的是连在A点的这个电路是往下连3个的,那么一旦转子往下转动一个,不是B连接到了D点,而是B点得到了原来在A点的电路,那么B就会连到往下3个的那个地方,反之亦然。那么每个盘在初始状态的连接情况,就代表着这个盘26个点的电路连接状况,也就是密钥。
如果理解了这个工作原理,那么最后一个反射转子盘就非常好理解了,无非就是去掉了这个转子的右盘,而把左盘上的点两两连在一起,构成了13对,当然转动也会带来配对的改变。
而这四个可以转的盘什么时候转动呢?规则是这样的:每处理完一个字符,第1个转子盘逆时针转一个字符,如果第1个转子盘转了26下,也就是处理完26个字符,第二个转子盘逆时针转动一个字符,然后第二个转26下第三个就转一个字符,第四个亦然。当然我们最开始可以把每个盘都拨动若干个字符,这个拨动不算转动次数。
以上就是对于这个机器的工作原理的解释,也是这个题最核心的地方,只要弄懂了这一点,这个题就是水题了。
题意:现在给你这么一个机器,首先告诉你四个盘的密钥(它对于每条密钥,是按每行26个字符给的,第x行第i个字符代表着字母‘a’+i-1在初始状态下通过第x个盘应该变成什么),接着第五行告诉你那个固定的简单置换盘的对应关系(给的方式同上),接下来第六行给你一行四个字符,第i个字符表示初始状态下,第i个盘被拨动了c[i]-‘a’个字符。接下来第七行给你了一段明文,第八行给你了这段明文在这个机器如上的状态下被加密之后的密文。然后现在告诉你,这上面八行字符串里面有至多3个字符被弄得看不清了,所以读入的时候用‘?’代替了,那么请你找出这三个‘?’应该对应的正确字符后,输出完整的明文(题目保证每组测试数据有且仅有一解)。
那么这个密文在题目中的运行顺序是什么呢:
1、每个字符首先正向通过简单置换板
2、通过步骤1得到的字符再依次正向通过1、2、3这三个转子置换板
3、通过步骤2得到的字符再通过反射转子置换板
4、通过步骤3得到的字符再依次逆向通过3、2、1这三个转子置换板
5、通过步骤4得到的字符再逆向通过简单置换板得到明文
6、每个字符完成上述五步之后,各个转子转动,为下一个字符的处理做准备。
思路:拿到这个题首先分析,只有3个字符不确定,而且每个之后26种情况,所以总共只有26*26*26=17526种可能性,完全可以枚举出来然后一一检测是否能满足解密过程。
于是就愉快地用dfs枚举然后检测了。
下面贴代码。
#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <map>
#include <vector>
#include <iostream>
#include <algorithm>
#define moo 1000000007//10^9+7
#define PI acos(-1.0)
using namespace std;
char s[10][100];//存最原始的8行字符串
int a[10][100];//存处理后的8行字符串,处理方法是对每个字符-'a'
struct question
{
int x;
int y;
}que[5];//存问号在的位置,第X行第Y个字符
int cou;//存问号的数量
int cheek()//检测函数,对于当前枚举的情况,如果解密正确则返回1,否则返回0
{
int b1[100];
int b2[100];//将明文密文取出,因为要做修改,所以避免对原数据造成影响。
int len=strlen(s[7]);
for(int i=0;i<len;i++)
{
b1[i]=a[4][a[7][i]];//将密文第一次通过简单置换板的操作顺手做了
b2[i]=a[6][i];
}
int d[4][30];//存每个转子正向通过时的电路图
int e[4][30];//存每个转子逆向通过时的电路图
for(int i=0;i<4;i++)
{
for(int j=0;j<26;j++)
{
int t=a[i][j];
d[i][j]=t-j;//正向通过,从j变成t,电路是+(t-j)
e[i][t]=j-t;//逆向通过,从t变成j,电路是+(j-t)
}
}
int c[4];//存的是每个转子置换板当前的转动情况。
for(int i=0;i<4;i++)
c[i]=a[5][i];
for(int i=0;i<len;i++)
{
for(int j=0;j<=3;j++)
{
b1[i]+=d[j][(b1[i]+c[j]+26)%26];
b1[i]=(b1[i]+26)%26;
}//当前字符依次正向通过1、2、3这三个板,因为反射板工作原理与普通的没什么两样,所以也顺手正向通过
for(int j=2;j>=0;j--)
{
b1[i]+=e[j][(b1[i]+c[j]+26)%26];
b1[i]=(b1[i]+26)%26;
}//然后再逆向通过3、2、1这三个板。
for(int j=0;j<26;j++)//判断这个字符逆向通过简单置换板之后是不是得到明文,如果不是,则当前枚举错误
if(b1[i]==a[4][j]&&b2[i]!=j)
return 0;
c[0]++;//对于每个转子做相应转动,为处理下一个字符做准备
if(c[0]==a[5][0]+26)
{
c[0]=a[5][0];
c[1]++;
if(c[1]==a[5][1]+26)
{
c[1]=a[5][1];
c[2]++;
if(c[2]==a[5][2]+26)
{
c[2]=a[5][2];
c[3]++;
if(c[3]==a[5][3]+26)
c[3]=a[5][3];
}
}
}
}
return 1;
}
int dfs(int x)
{
if(x==cou)
{
if(cheek()==1)
return 1;
return 0;
}
for(int i=0;i<26;i++)//枚举每一位填'a'+i的情况
{
a[que[x+1].x][que[x+1].y]=i;
if(dfs(x+1)==1)
return 1;
}
return 0;
}
void init()
{//预处理八行字符串,把所有点都处理成int型,方便操作,并且把'?'都提取出来
for(int i=0;i<8;i++)
{
int len=strlen(s[i]);
for(int j=0;j<len;j++)
{
if(s[i][j]=='?')
{
cou++;
que[cou].x=i;
que[cou].y=j;
}
else
a[i][j]=s[i][j]-'a';
}
}
}
int main()
{
int T;
cin>>T;
int dd=T;
while(T--)
{
for(int i=0;i<8;i++)
scanf("%s",s[i]);
cou=0;
init();
dfs(0);
printf("Scenario #%d:\n",dd-T);
int len=strlen(s[6]);
for(int i=0;i<len;i++)
printf("%c",a[6][i]+'a');
printf("\n\n");
}
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。
POJ1449 & ZOJ1036 Enigma(简单枚举)
原文:http://blog.csdn.net/zip_fan/article/details/46842233