Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.


To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.

Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.

The moment of inertia I of a set of n stars can be calculated with the formula


where w_i is the weight of star i, d_i is the distance form star i to the mass of center.

As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.

Now, you are supposed to calculate the minimum moment of inertia after transportation.

The first line contains an integer T (T ≤ 10), denoting the number of the test cases.

For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.

For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.

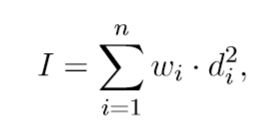
2
3 2
-1 0 1
4 2
-2 -1 1 2

0
0.5

2014 Asia AnShan Regional Contest

#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstdio>
using namespace std;

int main()
{
    int t,n,k;
    long long int p[50000+10];
    long long int d[50000+10];
    long long int ds[50000+10];
    double center;
    double minn=0,temp;
    cin>>t;
    while(t--)
    {
        minn=9999999999999999;
        cin>>n>>k;
        for(int i=1;i<=n;i++)
            cin>>p[i];
        sort(p+1,p+n+1);
        if(n==k||n-k==1)
        {
            printf("0\n");
            continue;
        }
        d[0]=0;
        ds[0]=0;
        for(int i=1;i<=n;i++)
        {
            d[i]=d[i-1]+p[i];
            ds[i]=ds[i-1]+p[i]*p[i];
        }
        for(int i=0;i<=k;i++)
        {
            center=(d[i+n-k]-d[i])*1.0/(n-k);
            temp=(ds[i+n-k]-ds[i])-2*center*(d[i+n-k]-d[i])+(n-k)*center*center;
            if(temp<minn)
                minn=temp;
        }
        printf("%.9f\n",minn);
    }
    return 0;
}