ex_GCD
逆元,ex_GCD
卡特兰数
假设,依次放1-n,放第一排记为0,放第二排记为1,题目的条件就转化为卡特兰数的条件了
附:线性求逆元,卡特兰数(递推)
p[1] = 1; for (int i = 2; i < 1000003; i++) { p[i] = - (MODP / i) * p[MODP % i]; p[i] = (p[i] % MODP + MODP) % MODP; }
f[1] = 1; for (int i = 2; i < 1000001; i++) { f[i] = ((f[i - 1] * ((long long)(4 * i - 2))) % MODP * p[i + 1]) % MODP; }
中国剩余定理(不互质)
一个一个来,解二元同余方程组
单个欧拉函数
线性求欧拉函数
扩展欧拉公式
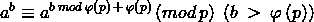
如果有人找到这个的证明,请告诉我,谢谢!
原文:http://www.cnblogs.com/89yanyu/p/4606364.html