象棋中的皇后（UVa 11538）

 【题目描述】

    你可能知道象棋怎么下以及皇后的移动规则。当两个皇后在同一行、同一列或同一条斜线上时，她们就会互相攻击。假设两个这样的皇后（一黑一白）被放在一个2×2的棋盘上，她们可以有12种互相攻击的方式，请看下图：

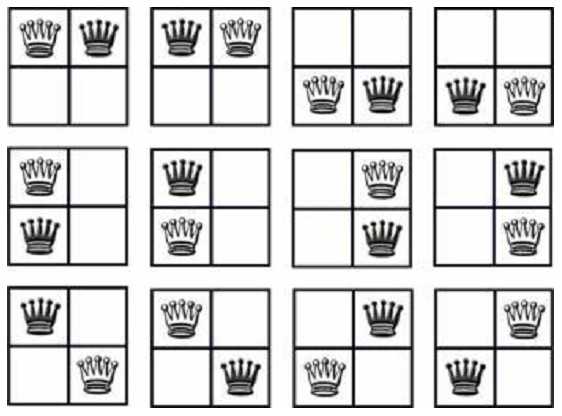
给出一个N×M的棋盘，计算有多少种放法能使两个皇后互相攻击。

【输入】

    输入至多包含5000行。每一行有两个非负整数N、M（0<M, N≤10⁶）。输入以两个N=M=0为结束标志，这一行不需要处理。

【输出】

    对于输入的每一行，输出一行。这一行包含一个整数，它表示放法的种数。所有的输出数据都在带符号的64位整数内。

【分析】

    这道题很明显是组合数学问题。

    首先，皇后间攻击当且仅当她们在同一行、同一列或同一斜线。对于每一个不同的位置，放置的方案都是不同的，也就是说，每一种方案间都没有交集，因此，我们可以用加法原理来解决。

    那么，我们可以分三种情况讨论：皇后在同一行、同一列和同一斜线。这里规定m>n，这样就省去了讨论m≤n，并且规定m为列数，n为行数。

(I)皇后在同一行。这种情况很容易想：若一个皇后放了一个位置，则另一个皇后只有(m-1)种放法。∴总放法为mn(m-1)。

(II)皇后在同一列。这种情况也很容易想：若一个皇后放了一个位置，则另一个皇后只有(n-1)种放法。∴总放法为mn(n-1)。

(III)皇后在同一斜线上。这种情况就有点复杂了。我们来详细讨论下：

    首先，我们把棋盘斜斜地切成一条条（先定一个方向，因为另一个方向是对称的）。接着，我们考虑一个问题——假设一条斜线长度为len，即这条斜线有len个格子，那么，当我们放了一个皇后之后，就剩下(len-1)个位置可以放，所以，每一条斜线的放置方案数为len×(len-1)。

    然后，我们再来算总方案数。假设我们切的方向是“／”，那么，左上角的斜线有长度为1, 2, 3, …, n-1的，所以方案总数为Σ[i(i-1)] (1≤i≤n-1)。注意到了吗？右下角有一模一样的情况，所以这里的方案总数也是Σ[i(i-1)] (1≤i≤n-1)。

    接下来，我们来讨论斜线长度为n的方案数——共有(m-n+1)条斜线，每条线上的方案数为n(n-1)，所以总方案数为(m-n+1)×n(n-1)。

    ∴一个方向的总方案数为2×Σ[i(i-1)] (1≤i≤n-1)+(m-n+1)×n(n-1)。

    又∵另一种情况与这种情况是对称的，∴最终的方案数Sum=2×{2×Σ[i(i-1)] (1≤i≤n-1)+(m-n+1)×n(n-1)}。

    然后就是数学的东西了——

Σ[i(i-1)]=Σ(i²-i)=Σ(i²)-Σ(i)

∵Σ(i²)  (1≤i≤n)=n(n+1)(2n+1)/6，Σ(i) (1≤i≤n)=n(n+1)/2

∴Σ(i²) (1≤i≤n-1)-Σ(i) (1≤i≤n-1)=n(n-1)(2n-1)/6-n(n-1)/2=[n(n-1)(2n-1)-3n(n-1)]/6=n(n-1)(2n-4)/6

∴Sum=2×[2×n(n-1)(2n-4)/6+(m-n+1)n(n-1)]=2×[2n(n-1)(n-2)/3+3(m-n+1)n(n-1)/3]=2/3×[2n(n-1)(n-2)+3(m-n+1)n(n-1)]=2/3×[2n(n-1)(n-2)+3(m-n+1)n(n-1)]=2/3×n(n-1)(3m-n+1)

那么，最终的答案Ans=Sum+mn(m-1)+mn(n-1)=2/3×n(n-1)(3m-n+1)+mn(m+

n-2)。这就是最终的公式。

【AC代码】

program chess;

var
  m,n:longint;
  q,r:qword;

procedure swap(var a,b:longint);  //这是防止m<=n用的
var k:longint;
begin
  k:=a; a:=b; b:=k;
end;

begin
  readln(n,m);
  while (n>0) and (m>0) do
  begin
    if n>m then swap(n,m);
    q:=m*n;
    q:=q*(n+m-2);
    r:=2*n*(n-1);
    r:=r*(3*m-n-1) div 3;  //以上4个语句就是公式，不过不知道为什么P很神经地返回错误215
    writeln(q+r);
    readln(n,m);
  end;
end.

象棋中的皇后（UVa 11538）,布布扣,bubuko.com

象棋中的皇后（UVa 11538）

原文：http://www.cnblogs.com/bigTG/p/3618361.html