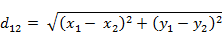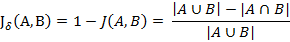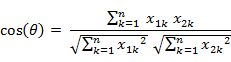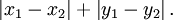总结了比较常用几种距离算法,如下:
1. 欧拉距离
欧拉距离是最经典的一种距离算法,适用于求解两点之间直线的距离,适用于各个向量标准统一的情况,如各种药品的使用量、商品的售销量等。
2. Pearson距离
Pearson是推荐时最常用的一种距离,对于评分、喜好等用户评判标准不一样的时候特别有用。可以化为两向量规范化后的乘积,其本质是两个向量是否同升同降。
Pearson相关系数:
3. 杰卡德距离
杰卡德距离在求两个集合的相交程度时比较有用,一般应用于布尔类型的向量中。应用场景,如两首音乐的被共同喜欢的程度、两个人性格的相似程度等
4. 夹角余弦距离
余弦距离不关心向量的长度,而只关心向量的夹角余弦。应用场景,如文本分类时,两文本之间距离计算。
5. 曼哈顿距离
曼哈顿距离,顾名思义,城市街区距离。主要应用场景,如棋盘、城市里两个点之间的距离等
6. 汉明距离
两个字符串之间的距离,用于计算之间的相似度。应用场景如钓鱼网站与正规网站之间相似程度、两作文是否作弊等。
计算方法,把S1变成S2所需要进行替换的最小次数。
几种常见距离算法小结,布布扣,bubuko.com
几种常见距离算法小结
原文:http://blog.csdn.net/codyshi/article/details/21412029