You have matrix a of size n?×?n. Let‘s number the rows of the matrix from 1 to n from top to bottom, let‘s number the columns from 1 to n from left to right. Let‘s use aij to represent the element on the intersection of the i-th row and the j-th column.
Matrix a meets the following two conditions:
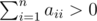 .
.Matrix b is strictly positive, if for any numbers i,?j (1?≤?i,?j?≤?n) the inequality bij?>?0 holds. You task is to determine if there is such integer k?≥?1, that matrix ak is strictly positive.
The first line contains integer n (2?≤?n?≤?2000) — the number of rows and columns in matrix a.
The next n lines contain the description of the rows of matrix a.
The i-th line contains n non-negative
integers ai1,?ai2,?...,?ain (0?≤?aij?≤?50).
It is guaranteed that 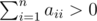 .
.
If there is a positive integer k?≥?1, such that matrix ak is strictly positive, print "YES" (without the quotes). Otherwise, print "NO" (without the quotes).
2 1 0 0 1
NO
5 4 5 6 1 2 1 2 3 4 5 6 4 1 2 4 1 1 1 1 1 4 4 4 4 4
YES
图论知识,一张图的邻接矩阵描述了点与点之间的可达关系,其k次幂表示了长度为k的路径的可达性。很明确,如果存在题目要求的k,即任意两点可达,a^k 就是一张有向完全图。
解法:
图的任意点的可达性算法比较多,稍微列于下...
Floyd算法:三个循环,求解图的最短路算法,O(n^3)。
Warshall 算法:求解二元关系的传递闭包,和Floyd算法有点类似,O(n^3)。可以尝试把矩阵变成布尔矩阵,利用位运算加速计算,貌似亦可解决此题。
然而,如果仅仅纠结于可达性,这道题就基本卡死了。因为可达性算法多数都是O(n^3),再怎么剪枝优化也几乎超时。因此,需要考虑有向完全图。
既然a^k 是有向完全图,那么对于a应该是有且仅有一个强连通分量,tarjan算法,O(|V|+|E|),over.
总结来说:tarjan算法是深度优先搜索算法,其结果只是强联通关系,信息量少,复杂度相对较低。而可达性算法,对每两个点之间的可达性都需要做出描述,信息量大,复杂度高,因此从这一点来说,解决一个问题可以从信息量的角度去选择比较合适的算法。
Codeforces Round #236 (Div. 2) E. Strictly Positive Matrix,布布扣,bubuko.com
Codeforces Round #236 (Div. 2) E. Strictly Positive Matrix
原文:http://blog.csdn.net/kevinkitty_love/article/details/21396509