POJ 1038 状态压缩dp

Description

Bugs Integrated, Inc. is a major manufacturer of advanced memory chips. They are launching production of a new six terabyte Q-RAM chip. Each chip consists of six unit squares arranged in a form of a 2*3 rectangle. The way Q-RAM chips are made is such that one takes a rectangular plate of silicon divided into N*M unit squares. Then all squares are tested carefully and the bad ones are marked with a black marker.

Finally, the plate of silicon is cut into memory chips. Each chip consists of 2*3 (or 3*2) unit squares. Of course, no chip can contain any bad (marked) squares. It might not be possible to cut the plate so that every good unit square is a part of some memory chip. The corporation wants to waste as little good squares as possible. Therefore they would like to know how to cut the plate to make the maximum number of chips possible.
Task
You are given the dimensions of several silicon plates and a list of all bad unit squares for each plate. Your task is to write a program that computes for each plate the maximum number of chips that can be cut out of the plate.

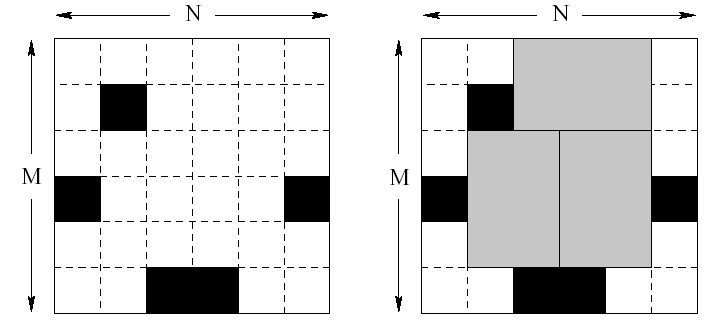
Input

Output

Sample Input

2
6 6 5
1 4
4 6
2 2
3 6
6 4
6 5 4
3 3
6 1
6 2
6 4

Sample Output

3
4

题意：给定n*m的一个区域，有若干损坏的格子，用2*3的砖铺，最多放多少块砖。

三进制压缩dp，研究好久，仍感吃力，只好硬着头皮往下坚持。

代码：

/* ***********************************************
Author :rabbit
Created Time :2014/3/14 15:40:30
File Name :F.cpp
************************************************ */
#pragma comment(linker, "/STACK:102400000,102400000")
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <string>
#include <time.h>
#include <math.h>
#include <queue>
#include <stack>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define eps 1e-8
#define pi acos(-1.0)
typedef long long ll;
const int maxn=60010;
int vis[155][15],dp[2][maxn],A[11],P[11],Q[11];
int n,m,K,mask;
int getstate(int f[]){
	int res=0;
	for(int i=1;i<=m;i++)res+=f[i]*A[i-1];
	return res;
}
void getback(int x,int f[]){
	for(int i=1;i<=m;i++)f[i]=x%3,x/=3;
}
void dfs(int i,int x,int num){//:i，i-1层都空；1：i层为空，i-1层被占；2：i层被占。
	if(x>m)return;
	int cur=(i+1)&1,nxt=i&1,k=getstate(Q);
	dp[nxt][k]=max(dp[nxt][k],dp[cur][getstate(P)]);
	if(x<=m-1&&(P[x]==0&&P[x+1]==0)&&(Q[x]==0&&Q[x+1]==0)){
		Q[x]=Q[x+1]=2;
		int kk=getstate(Q);
		dp[nxt][kk]=max(dp[nxt][kk],num+1);
		dfs(i,x+2,num+1);
		Q[x]=Q[x+1]=0;
	}
	if(x<=m-2&&(!Q[x]&&!Q[x+1]&&!Q[x+2])){
		Q[x]=Q[x+1]=Q[x+2]=2;
		int kk=getstate(Q);
		dp[nxt][kk]=max(dp[nxt][kk],num+1);
		dfs(i,x+3,num+1);
		Q[x]=Q[x+1]=Q[x+2]=0;
	}
	dfs(i,x+1,num);
}
int main()
{
     //freopen("data.in","r",stdin);
     //freopen("data.out","w",stdout);
     A[0]=1;for(int i=1;i<=10;i++)A[i]=3*A[i-1];
	 int T;scanf("%d",&T);
	 while(T--){
		 scanf("%d%d%d",&n,&m,&K);int x,y;
		 memset(vis,0,sizeof(vis));
		 for(int i=0;i<K;i++){
			 scanf("%d%d",&x,&y);
			 vis[x][y]=1;
		 }
	 	 memset(dp,-1,sizeof(dp));
		 memset(P,0,sizeof(P));
		 memset(Q,0,sizeof(Q));
		 for(int i=1;i<=m;i++)P[i]=vis[1][i]+1;
		 dp[1][getstate(P)]=0;
		 mask=A[m];
		 for(int i=2;i<=n;i++){
			 int cur=(i+1)&1,nxt=i&1;
			 memset(dp[nxt],-1,sizeof(dp[nxt]));
			 for(int j=0;j<mask;j++){
				 if(dp[cur][j]==-1)continue;
				 getback(j,P);
				 for(int x=1;x<=m;x++){
					 if(vis[i][x])Q[x]=2;
					 else{
						 Q[x]=P[x]-1;
						 if(Q[x]<0)Q[x]=0;
					 }
				 }
				 dfs(i,1,dp[cur][j]);
			 }
		 }
		 int ans=0;
		 for(int i=0;i<mask;i++)ans=max(ans,max(dp[0][i],dp[1][i]));
		 cout<<ans<<endl;
	 }
     return 0;
}

POJ 1038 状态压缩dp,布布扣,bubuko.com

POJ 1038 状态压缩dp

原文：http://blog.csdn.net/xianxingwuguan1/article/details/21240063