统计学习方法是基于训练数据构建统计模型,从而对数据进行预测和分析。
统计学习分为,监督学习(supervised
learning),非监督学习,半监督学习和强化学习(reinforcement
learning),其中以监督学习最为常见和重要,所以这里只讨论监督学习
统计学习的过程如下,
1. 获取训练数据集合
2. 确定假设空间,即所有可能的模型的集合
3.
确定模型选择的准则(什么是最优模型的标准),即学习的策略
4. 实现求解最优模型的算法(如何获取最优模型),即学习的算法
5. 通过算法中假设空间中,找到最优模型
6. 使用该模型对新数据进行预测和分析
输入数据
输入实例x记作,
联合概率分布
监督学习假设输入和输出的随机变量X和Y遵循联合概率分布P(X,Y),P(X,Y)表示分布函数或分布密度函数。
这个是基本假设,即输入和输出数据间是存在某种规律和联系的,否则如果完全随机的,就谈不上学习了。并且训练数据和测试数据是依据P(X,Y)独立同分布产生的
假设空间
监督学习的目的在于学习一个由输入到输出的映射,这个映射由模型来表示。
而这样的模型不只一个,可能很多,所有可能的模型的集合就是假设空间(hypothesis space).
假设空间代表了学习的范围,监督学习的目的就是从假设空间中找到最优的模型
模型
在监督学习中,模型有两类
非概率模型,决策函数 
概率模型,条件概率 
策略
如何定义一个模型好坏?
损失函数(L(Y,f(X)),度量一次预测的结果好坏,即表示预测值f(X)和真实值Y之间的差异程度。  其他几个损失函数都比较好理解
其他几个损失函数都比较好理解
对数损失函数,解释一下
首先它用于概率模型,最精确的预测P(Y|X)=1,所以为1时L=0,没有损失
而P都是小于1,所以对数为负,并且越小L的值越大,想想对数分布曲线
风险函数(risk function)或期望损失(expected loss)
用于度量平均预测结果的好坏,其实就是损失函数的期望
输入X,输出Y遵循联合分布P(X,Y),定义如下 ![]()
数学期望
参考http://zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E6%9C%9F%E6%9C%9B期望就是求平均值,对于离散值很简单,乘上概率相加就可以,比如抛骰子的期望就是,
对于连续数据,稍微复杂些,需要使用积分,本质还是一样的。
积分参考,http://zh.wikipedia.org/wiki/%E7%A7%AF%E5%88%86
上面说了风险函数代码了模型的平均的预测结果,所以学习的目标应该是选择风险函数最小的模型。
但是问题在于,计算风险函数需要知道联合分布P(X,Y),但是这个是无法知道的,否则也不用学习了,所以监督学习就成了一个病态问题(ill-formed
problem),即无法精确的判断模型真正的效果
经验风险(empirical risk或经验损失(empirical loss)
既然无法得到真正的风险函数的值,我们就用训练数据集上的平均损失来模拟真正的风险函数 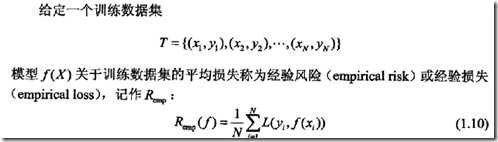
当N无穷大的时候,经验风险会逼近期望风险
所以我们可以采用经验风险最小化(empirical risk minimization,
ERM)的策略来找到最优的模型,当样本容量足够大的时候,能保证很好的学习效果
在现实中被广泛使用,比如,极大似然估计(maximum
likelihood estimation)
当然这种策略的问题就是会导致过拟合(over-fitting)现象
所以提出结构风险最小化(structural risk
minimization,SRM)策略来防止过拟合 ![]()
其实思路很简单,就是在经验风险后面加上表示模型复杂度的正则化项(regularizer)或罚项(penalty
term),其中J(f)表示模型复杂度,模型越复杂就越大
因为越是过拟合的模型越是复杂,所以通过regularizer可以有效平衡拟合程度
算法
用什么样的方法来求解最优模型
这样统计学习模型就归结为最优化问题,如果最优化问题有显式的解析解,比较简单,直接求出即可。但通常解析解是不存在的,所以就需要利用最优化算法来求解。
过拟合与模型选择
再仔细分析一下过拟合问题
当我们在假设空间中,选择模型的时候,希望可以尽可能逼近那个“真”模型,具体上讲就是两个模型间,参数个数相同,并且参数向量相近
但是如果在选择的时候一味的提高对训练集的预测能力,会导致得到比真模型复杂度更高的模型,即包含更多的参数,称为过拟合
例子,用M次多项式去拟合图中训练集中的10数据点 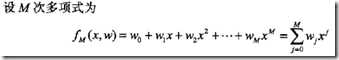
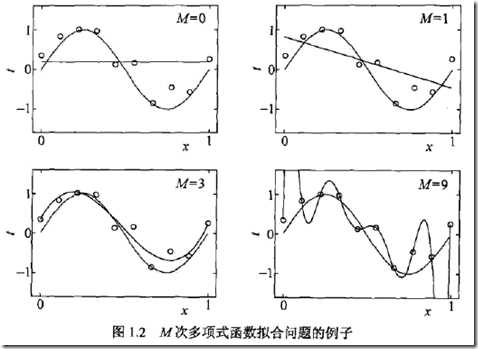
可以看到当多项式参数个数为0,1时拟合效果是很差的
但当为9时,完美的经过训练集中的每个点,但因为训练集是有噪点的,所以这个模型过于复杂,拟合程度也不好,这就是过拟合
只有当为3时,达到很好的拟合效果
如下图,当训练误差接近于0的时候,模型复杂度会大大增加,并且测试误差也会变大,所以必须要找到那个平衡点上的模型
问题是如何找到,下面有两个方法
正则法
这个方法前面提过 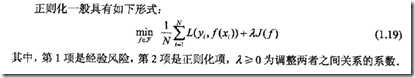
正则项可以有不同的形式,比如在回归问题中,损失函数是平方损失,正则项可以是参数向量的L1范数或L2范数
具体定义参考下面,反正都可以代表模型的复杂度
给定向量x=(x1,x2,...xn)
L1范数:向量各个元素绝对值之和,曼哈頓距離
L2范数:向量各个元素的平方求和然后求平方根,歐幾里得距離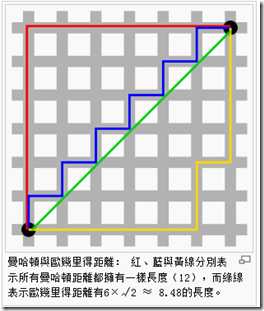
正则法是符合奥卡姆剃刀(Occam’s razor,http://zh.wikipedia.org/zh/%E5%A5%A5%E5%8D%A1%E5%A7%86%E5%89%83%E5%88%80)原理的,优先选择更简单的模型
交叉验证
1. 简单交叉验证,将数据70%作为训练集,30%作为测试集,然后选出测试误差最小的模型
2.
S-fold交叉验证,将数据随机分成S份,将S-1份作为训练集,剩下的作为测试集,对于训练集和测试集有S种选择,所以选出S次评测的平均误差最小的模型
3. leave-one-out交叉验证,S-fold的特例,用于数据缺乏的情况,S=N,即一份里面只有一个数据
泛化能力(generalization ability)
学习方法的泛化能力指该方法学习到的模型对未知数据的预测能力
往往采用通过测试误差来评价学习方法的泛化能力,问题是过于依赖测试集,并且测试集是有限的,不是很可靠
泛化误差(generalization error),即模型的期望风险 ![]()
原文:http://www.cnblogs.com/fxjwind/p/3601119.html