回归分析（regression analysis)是确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法。按照涉及的自变量的多少，可分为一元回归分析和多元回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

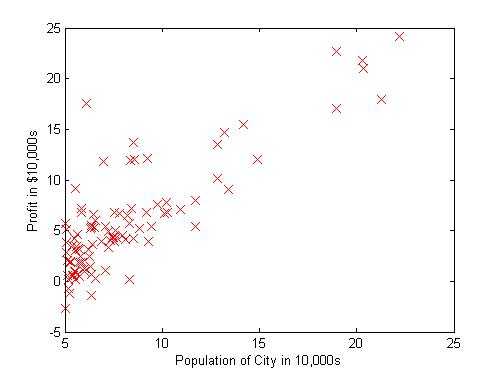
假设现在的目标是开餐馆选址，自变量x是当地人口，因变量y是选址此处所获利润。拟合直线为 $h_{\theta}(x)=\theta _0 +\theta _1 * x$ ，我们用梯度下降法来确定θ。

代价函数

我们的目标是找到合适的θ，让确定的直线与样本数据之间的差距最小，这个差距用代价函数来衡量。对第 i 个样本 $x^{(i)}$ ，我们将代价定为估计值 $h_{\theta}(x^{(i)})$ 与实际值 $y^{(i)}$ 的差的平方。假设我们的样本数为m个，于是代价函数为：

$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$

其中1/2是为了接下来求导时消去常数项。需要注意的是，这里的自变量是θ而非x，可以看做x是已知的常数。

将θ看做二维平面坐标，J看做第三维的值。将J展开后，θ的每一维最高都是二次幂，也即从每个切面看，J(θ)都是一条抛物线，所以J构成的平面将会成为一个类似碗的形状，存在全局最小值。

梯度下降

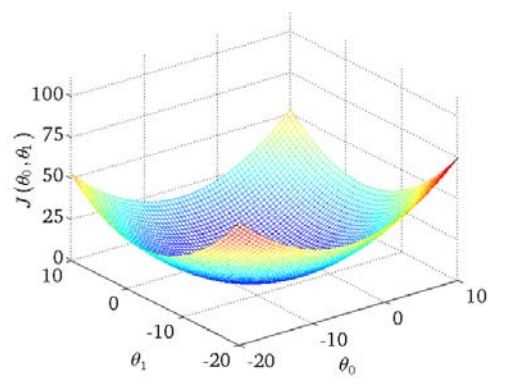
从J的三维图中可以看出，假如θ_j偏大，那么J对θ_j的偏导数就为正，反之为负。我们利用这个特性来估计θ参数。对J求θ₀与θ₁的偏导数，再设置一个合适的学习率α对θ进行迭代，从而近似出最终的θ：

$\theta_{j}:=\theta_{j} - \alpha*\frac{\partial J(\theta)}{\partial \theta_{j}}$

展开得到：

$\theta_{j}:=\theta_{j} - \frac{\alpha}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$

当接近最低点时，对应的偏导数绝对值也会变小，降低了θ的收敛速度，因此学习率α在迭代过程中不需要调整，不必担心矫枉过正。

梯度下降法解线性回归,布布扣,bubuko.com

梯度下降法解线性回归

原文：http://www.cnblogs.com/ericxing/p/3597139.html