问题描述:考察一个机械厂,其中有 m 台一模一样的机器。现有 n 个作业需要处理,设作业 i 的处理时间为ti,这个时间为从将作业放入机器直到从机器上取下作业的时间。所谓调度(s c h e d u l e)是指按作业在机器上的运行时间对作业进行分配,使得:
• 一台机器在同一时间内只能处理一个作业。
• 一个作业不能同时在两台机器上处理。
• 作业i 一旦运行,则需要ti个时间单位。
我们的任务是写一个程序,以便确定如何进行调度才能使在 m 台机器上执行给定的n 个作
业时所需要的处理时间最短。建立这种调度非常难。实际上,没有人能够设计一个具有多项
式时间复杂性的算法(即一个复杂性为 O (nk ml ) 的算法, k 和l 为常数)来解决最小调度时间
问题。
在调度问题中,采用了一个称为最长处理时间优先( longest processing time first, LPT)的
简单调度策略,它可以帮助我们获得一个较理想的调度长度,该长度为最优调度长度的 4 / 3 -
1 / ( 3m)。在L P T算法中,作业按它们所需处理时间的递减顺序排列。在分配一个作业时,总是
将其分配给最先变为空闲的机器。
利用堆可在 O (nl o gn) 时间内建立L P T调度方案。首先,当 n≤m时,只需要将作业 i在0~ti 时刻内分配到机器 i 上去处理。当n >m时,可以首先利用H e a p S o r t将作业按处理时间递增的顺序排列。为了建立L P T调度,作业按相反次序进行分配。
实现:

1 #ifndef LPT_H 2 #define LPT_H 3 #include "MinHeap.h" 4 #include "MaxHeap.h" 5 using namespace std; 6 template<typename T> 7 void HeapSort(T a[], int n); 8 9 class JobNode 10 { 11 friend void LPT(JobNode*, int, int); 12 friend void HeapSort<>(JobNode a[], int n); 13 friend bool operator< (const JobNode& lhs,const JobNode& rhs) 14 { 15 return lhs.time < rhs.time ? true : false; 16 } 17 friend bool operator> (const JobNode& lhs, const JobNode& rhs) 18 { 19 return lhs.time > rhs.time ? true : false; 20 } 21 friend bool operator== (const JobNode& lhs, const JobNode& rhs) 22 { 23 return lhs.time == rhs.time ? true : false; 24 } 25 public: 26 JobNode() :ID(0), time(0){}; 27 JobNode(const int& id, const int& t) :ID(id), time(t){}; 28 operator int() const{ return time; } 29 operator int*() { 30 return &time; } 31 32 33 private: 34 int ID; 35 int time; 36 }; 37 38 class MachineNode 39 { 40 friend void LPT(JobNode*, int, int); 41 friend bool operator< (const MachineNode& lhs, const MachineNode& rhs) 42 { 43 return lhs.avail < rhs.avail ? true : false; 44 } 45 friend bool operator> (const MachineNode& lhs, const MachineNode& rhs) 46 { 47 return lhs.avail > rhs.avail ? true : false; 48 } 49 friend bool operator== (const MachineNode& lhs, const MachineNode& rhs) 50 { 51 return lhs.avail == rhs.avail ? true : false; 52 } 53 public: 54 operator int() const{ return avail; } 55 private: 56 int ID; 57 int avail; 58 }; 59 60 61 template<typename T> 62 void HeapSort(T a[], int n) 63 { 64 if (a == NULL || n <= 0) 65 { 66 throw exception("Invalid input"); 67 } 68 69 MaxHeap<T> H(1); 70 H.Initialize(a, n, n); 71 72 for (int i = 0; i < n; ++i) 73 { 74 H.DeleteMax(a[i]); 75 } 76 } 77 78 //n为作业数,m为机器数 79 void LPT(JobNode a[], int n, int m) 80 { 81 82 if (n <= m) 83 { 84 cout << "Schedule one job per machine" << endl; 85 return; 86 } 87 88 HeapSort(a, n);//将作业时长排序 89 90 MinHeap<MachineNode> H(m); 91 MachineNode x; 92 for (int i = 1; i <= m; ++i) 93 { 94 x.avail = 0; 95 x.ID = i; 96 H.Insert(x); 97 } 98 99 for (int i = 0; i < n; ++i) 100 { 101 H.DeleteMin(x);//取出第一个空闲的机器 102 cout << "Schedule job " << a[i].ID << " on machine" 103 << x.ID << " from " << x.avail << " to " << (x.avail + a[i].time) << endl; 104 105 x.avail += a[i].time; 106 H.Insert(x); 107 } 108 } 109 110 #endif
最大堆:

1 #ifndef MAXHEAP_H 2 #define MAXHEAP_H 3 4 #include<iostream> 5 #include<algorithm> 6 #include "exceptionerror.h" 7 using namespace std; 8 9 template<typename T> 10 class MaxHeap 11 { 12 public: 13 MaxHeap(int MaxHeapSize = 10); 14 ~MaxHeap() 15 { 16 if (heap!=NULL) 17 { 18 delete[] heap; 19 heap = NULL; 20 } 21 } 22 23 int Size() const{ return CurrentSize; } 24 T Max() 25 { 26 if (CurrentSize==0) 27 { 28 throw OutofBounds(); 29 } 30 31 return heap[1]; 32 } 33 34 MaxHeap<T>& Insert(const T& x); 35 MaxHeap<T>& DeleteMax(T& x); 36 void Initialize(T a[], int size, int ArraySize); 37 private: 38 int CurrentSize; 39 int MaxSize; 40 T* heap; 41 }; 42 43 template<typename T> 44 MaxHeap<T>::MaxHeap(int MaxHeapSize=10):MaxSize(MaxHeapSize),CurrentSize(0) 45 { 46 heap = new T[MaxSize + 1]; 47 } 48 49 template<typename T> 50 MaxHeap<T>& MaxHeap<T>::Insert(const T& x) 51 { 52 size_t index = ++CurrentSize; 53 while (index!=1&&x>heap[index/2]) 54 { 55 heap[index] = heap[index / 2]; 56 index = index / 2;//移向父节点 57 } 58 59 heap[index] = x; 60 61 return *this; 62 } 63 64 template<typename T> 65 MaxHeap<T>& MaxHeap<T>::DeleteMax(T& x) 66 { 67 if (CurrentSize==0) 68 { 69 throw OutofBounds(); 70 } 71 72 x = heap[1]; 73 T temp = heap[CurrentSize--]; 74 size_t index = 1; 75 size_t cindex = 2; 76 while(cindex<=CurrentSize) 77 { 78 if (cindex<CurrentSize&&heap[cindex]<heap[cindex+1]) 79 { 80 ++cindex; 81 } 82 83 if (temp>heap[cindex]) 84 { 85 break; 86 } 87 88 heap[index] = heap[cindex];//move down 89 index = cindex; 90 cindex *= 2; 91 } 92 93 heap[index] = temp; 94 return *this; 95 } 96 97 template<typename T> 98 void MaxHeap<T>::Initialize(T a[], int size, int ArraySize) 99 { 100 delete[] heap; 101 heap = new T[ArraySize + 1]; 102 MaxSize = ArraySize; 103 CurrentSize = size; 104 105 memcpy(heap+1, a, (CurrentSize)*sizeof(T)); 106 size_t cindex; 107 for (size_t index = CurrentSize / 2; index >= 1;--index) 108 { 109 T temp = heap[index]; 110 111 cindex = 2 * index; 112 while (cindex<=CurrentSize) 113 { 114 if (cindex<CurrentSize&&heap[cindex + 1]>heap[cindex]) 115 { 116 ++cindex; 117 } 118 119 if (temp>heap[cindex]) 120 { 121 break; 122 } 123 124 heap[cindex/2] = heap[cindex]; 125 cindex *= 2; 126 } 127 128 heap[cindex / 2] = temp; 129 } 130 131 } 132 #endif
最小堆:

1 #ifndef MinHeap_H 2 #define MinHeap_H 3 4 #include<iostream> 5 #include<algorithm> 6 #include "exceptionerror.h" 7 using namespace std; 8 9 template<typename T> 10 class MinHeap 11 { 12 public: 13 MinHeap(int MaxHeapSize = 10); 14 ~MinHeap() 15 { 16 if (heap!=NULL) 17 { 18 delete[] heap; 19 heap = NULL; 20 } 21 } 22 23 int Size() const{ return CurrentSize; } 24 T Min() 25 { 26 if (CurrentSize==0) 27 { 28 throw OutofBounds(); 29 } 30 31 return heap[1]; 32 } 33 34 MinHeap<T>& Insert(const T& x); 35 MinHeap<T>& DeleteMin(T& x); 36 void Initialize(T a[], int size, int ArraySize); 37 private: 38 int CurrentSize; 39 int MaxSize; 40 T* heap; 41 }; 42 43 template<typename T> 44 MinHeap<T>::MinHeap(int MaxHeapSize=10):MaxSize(MaxHeapSize),CurrentSize(0) 45 { 46 heap = new T[MaxSize + 1]; 47 } 48 49 template<typename T> 50 MinHeap<T>& MinHeap<T>::Insert(const T& x) 51 { 52 size_t index = ++CurrentSize; 53 while (index!=1&&x<heap[index/2]) 54 { 55 heap[index] = heap[index / 2]; 56 index = index / 2;//移向父节点 57 } 58 59 heap[index] = x; 60 61 return *this; 62 } 63 64 template<typename T> 65 MinHeap<T>& MinHeap<T>::DeleteMin(T& x) 66 { 67 if (CurrentSize==0) 68 { 69 throw OutofBounds(); 70 } 71 72 x = heap[1]; 73 T temp = heap[CurrentSize--]; 74 size_t index = 1; 75 size_t cindex = 2; 76 while(cindex<=CurrentSize) 77 { 78 if (cindex<CurrentSize&&heap[cindex]>heap[cindex+1]) 79 { 80 ++cindex; 81 } 82 83 if (temp<heap[cindex]) 84 { 85 break; 86 } 87 88 heap[index] = heap[cindex];//move down 89 index = cindex; 90 cindex *= 2; 91 } 92 93 heap[index] = temp; 94 return *this; 95 } 96 97 template<typename T> 98 void MinHeap<T>::Initialize(T a[], int size, int ArraySize) 99 { 100 delete[] heap; 101 heap = new T[ArraySize + 1]; 102 MaxSize = ArraySize; 103 CurrentSize = size; 104 105 memcpy(heap+1, a, (CurrentSize)*sizeof(T)); 106 size_t cindex; 107 for (size_t index = CurrentSize / 2; index >= 1;--index) 108 { 109 T temp = heap[index]; 110 111 cindex = 2 * index; 112 while (cindex<=CurrentSize) 113 { 114 if (cindex<CurrentSize&&heap[cindex + 1]<heap[cindex]) 115 { 116 ++cindex; 117 } 118 119 if (temp<heap[cindex]) 120 { 121 break; 122 } 123 124 heap[cindex/2] = heap[cindex]; 125 cindex *= 2; 126 } 127 128 heap[cindex / 2] = temp; 129 } 130 131 } 132 #endif
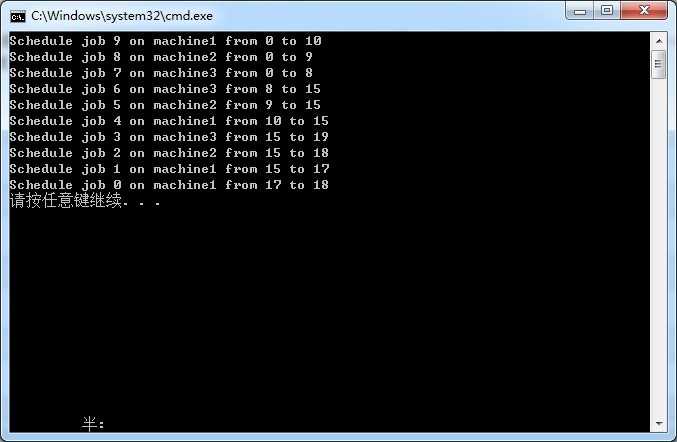
运行:

1 #include <iostream> 2 #include "LPT.h" 3 using namespace std; 4 5 6 int main() 7 { 8 JobNode a[10]; 9 for (int i = 0; i < 10;++i) 10 { 11 JobNode x(i, i + 1); 12 13 a[i] = x; 14 } 15 16 LPT(a, 10, 3); 17 18 return 0; 19 }
原文:http://www.cnblogs.com/haoliuhust/p/4371266.html