通常情况下的线性拟合不能很好地预测所有的值,因为它容易导致欠拟合(under fitting),比如数据集是
一个钟形的曲线。而多项式拟合能拟合所有数据,但是在预测新样本的时候又会变得很糟糕,因为它导致数据的
过拟合(overfitting),不符合数据真实的模型。
今天来讲一种非参数学习方法,叫做局部加权回归(LWR)。为什么局部加权回归叫做非参数学习方法呢? 首
先参数学习方法是这样一种方法:在训练完成所有数据后得到一系列训练参数,然后根据训练参数来预测新样本
的值,这时不再依赖之前的训练数据了,参数值是确定的。而非参数学习方法是这样一种算法:在预测新样本值
时候每次都会重新训练数据得到新的参数值,也就是说每次预测新样本都会依赖训练数据集合,所以每次得到的
参数值是不确定的。
接下来,介绍局部加权回归的原理。
之前在普通的线性拟合中,我们得到了最小二乘的损失函数为
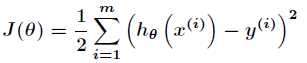
找到合适的参数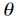 使得上述损失函数最小即可。而在局部加权回归中,损失函数变为
使得上述损失函数最小即可。而在局部加权回归中,损失函数变为
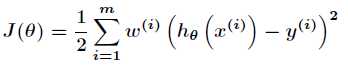
其中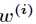 的表达式如下
的表达式如下
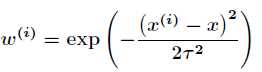
上式中参数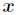 为新预测的样本特征数据,它是一个向量,参数
为新预测的样本特征数据,它是一个向量,参数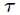 控制了权值变化的速率,权值有一个性质
控制了权值变化的速率,权值有一个性质
(1)如果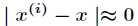 ,则
,则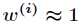 。
。
(2)如果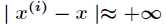 ,则
,则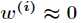 。
。
所以,对于离预测样本数据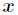 较近的点权值较大,离预测样本数据
较近的点权值较大,离预测样本数据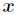 较远的点权值较小。
较远的点权值较小。
很明显,局部加权回归在每一次预测新样本时都会重新确定参数,以达到更好的预测效果。当数据规模比较大的
时候计算量很大,学习效率很低。并且局部加权回归也不是一定就是避免underfitting。
原文:http://blog.csdn.net/acdreamers/article/details/44662753