拓扑排序和关键路径

拓扑排序　

  　1. AOV网

　　在工程领域，一个大的工程项目通常被划分为许多较小的子工程（称为活动）。显然，当这些子工程都完成时，整个工程都完成了。在有向图中，若以顶点表示活动，用有向边表示活动之间的优先关系，则称这样的有向图为以顶点表示活动的网（AOV网）。AOV网中的弧表示了活动之间的优先关系，也可以说是一种活动进行时的制约关系；在AOV网中不应出现有向环。

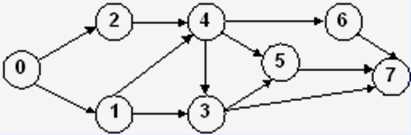
　　2. 拓扑排序及其算法

　　a. 在AOV网中选择一个入度为0（没有前驱）的顶点且输出它。

　　b. 从网中删除该顶点及其与该顶点有关的所有边。

　　c. 重复上述两步，直至网中不存在入读为0的顶点为止。

　　上图的拓扑序列有：02143567，01243657，02143657，01243567

关键路径

　　在AOV网络中，如果边上的权表示完成该活动所需的时间，则称这样的AOV为AOE网络。

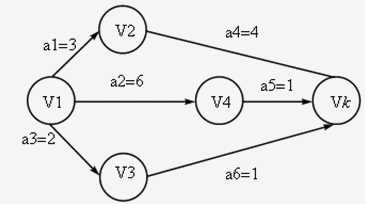
　　从源点到汇点的路径中，长度最长的路径称为关键路径。

　　关键路径的几个重要概念:

　　① 顶点j事件的最早发生时间：即从源点到顶点j的最长路径长度（时间），记作Ve(j); (PS:因为Vk事件必须在它的入度所表示的活动全部执行完成才能发生) 　　　　Ve(k) = a2 + a5 = 7;

　　② 活动ai的最早开始时间：Ve(j)是以顶点j为起点的出边所表示的活动ai的最早开始时间，记作e(i);　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  e(5) = Ve(4) = a2 = 6;

　　③ 顶点j事件的最迟发生时间：即在不推迟整个工程完成的前提下，一个事件j允许最迟的发生时间，记作Vl(j);　　　　　　　　　　　　　　　　　　　　　　　　　Vl(3) = Ve(k) - a6 = 7 - 1 = 6;

　　④ 活动ai的最迟开始时间：Vl(j)-(ai所需的时间)，就是活动ai的最迟开始时间，其中j是ai活动的终点，记作l(j)。　　　　　　　　　　　　　　　　　　　　　　　　l(k) = Vl(k) - a6 = 7 - 1 = 6;

拓扑排序和关键路径

原文：http://www.cnblogs.com/ImaY/p/4368170.html