| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 12603 | Accepted: 3367 |
Description
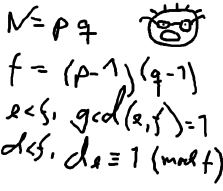The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. Input
Output
Sample Input
143 10 143 20 667 20 667 30 2573 30 2573 40 0 0
Sample Output
GOOD BAD 11 GOOD BAD 23 GOOD BAD 31
题意：一个整数K（大数）是两个素数A和B(A<=B)的乘积,满A<L则输出“GOOD”，否则输出“BAD”和A
思路：将K用字符串读取再转为千分制的数组K，利用同余模定理求余数判断能否被给定范围(2,L)中的某一素数整除
虽然思路参考了题解，但程序还是完全由自己写并一步一步调试成功的，庆祝一下！
#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #include<algorithm> using namespace std; const int maxn=1000100; const int INF=(1<<28); char Kc[maxn]; int K[maxn],len; int L; bool isprime[maxn]; int prime[maxn],cnt=0; void play_prime() { memset(isprime,1,sizeof(isprime)); //for(int i=1;i<=30;i++) cout<<isprime[i]<<endl; isprime[1]=0; for(int i=2;i<maxn;i++){ if(!isprime[i]) continue; for(int j=i*2;j<=maxn-i;j+=i){ isprime[j]=0; } } cnt=0; for(int i=1;i<maxn;i++){ if(isprime[i]) prime[cnt++]=i; } } int mod(int *K,int t) { int res=0; for(int i=len-1;i>=0;i--){ res=(res*1000+K[i])%t; } return res; } void debug_prime() { for(int i=0;i<100;i++){ cout<<prime[i]<<" "; if(i%10==0) cout<<endl; } } void debug_K() { for(int i=len-1;i>=0;i--) cout<<K[i]<<" "; cout<<endl; } int main() { play_prime(); //debug_prime(); while(scanf("%s%d",Kc,&L)!=EOF){ if(strcmp(Kc,"0")==0) break; len=0; for(int i=strlen(Kc)-1;i>=0;i-=3){ K[len++]=(Kc[i]-‘0‘)+(i-1>=0?(Kc[i-1]-‘0‘):0)*10+(i-2>=0?(Kc[i-2]-‘0‘):0)*100; } //debug_K(); bool flag=1; int ans; for(int i=0;i<cnt;i++){ if(prime[i]>=L) break; if(mod(K,prime[i])==0){ flag=0; ans=prime[i]; break; } } if(flag) cout<<"GOOD"<<endl; else cout<<"BAD "<<ans<<endl; } return 0; }
原文：http://www.cnblogs.com/--560/p/4366916.html
