一、题目:返回一个二维整数数组中最大子数组的和。
项目成员:檀威,陈志利
#include <iostream.h>
int maxSubArray(int **a,int n,int m)
{
int **p=new int*[n];
int i,j;
if(m==0||n==0)
return 0;
//计算p[i][j]
for(i=0;i<n;i++)
{
p[i]=new int[m];
for(j=0;j<m;j++)
{
if(i==0)
{
if(j==0)
p[i][j]=a[i][j];
else
p[i][j]=p[i][j-1]+a[i][j];
}
else
{
if(j==0)
p[i][j]=p[i-1][j]+a[i][j];
else
p[i][j]=p[i][j-1]+p[i-1][j]-p[i-1][j-1]+a[i][j];
}
}
}
//计算二维数组最大子数组的和
int temp;
int max=a[0][0];
int sum;
//如果m==1
if(m==1)
{
for(i=0;i<n;i++)
{
for(j=i;j<n;j++)
{
if(i==0)
{
temp=p[j][m-1];
}
else
{
temp=p[j][m-1]-p[i-1][m-1];
}
if(sum<temp)
sum=temp;
}
}
}
else
{
for(i=0;i<n;i++)
{
for(j=i;j<n;j++)
{
if(i==0)
{
temp=p[j][m-1]-p[j][m-2];
}
else
{
temp=p[j][m-1]-p[j][m-2]-p[i-1][m-1]+p[i-1][m-2];
}
for(int k=m-2;k>=0;k--)
{
if(temp<0)
temp=0;
if(i==0)
{
if(k==0)
temp+=p[j][k];
else
temp+=p[j][k]-p[j][k-1];
}
else
{
if(k==0)
temp+=p[j][k]-p[i-1][k];
else
temp+=p[j][k]-p[j][k-1]-p[i-1][k]+p[i-1][k-1];
}
if(sum<temp)
sum=temp;
}
}
}
}
return sum;
}
int main()
{
int n,m;
cout<<"请输入二维数组的行数:"<<endl;
cin>>n;
cout<<"请输入二维数组的列数"<<endl;
cin>>m;
int i,j;
int **a=new int*[n];
cout<<"请输入该二维数组元素:"<<endl;
for(i=0;i<n;i++)
{
a[i]=new int[m];
for(j=0;j<m;j++)
{
cin>>a[i][j];
}
}
int sum=maxSubArray(a,n,m);
cout<<"二维数组的最大子数组之和:"<<sum<<endl;
return 0;
}
四、测试及实验截图
有正有负时测试正确:
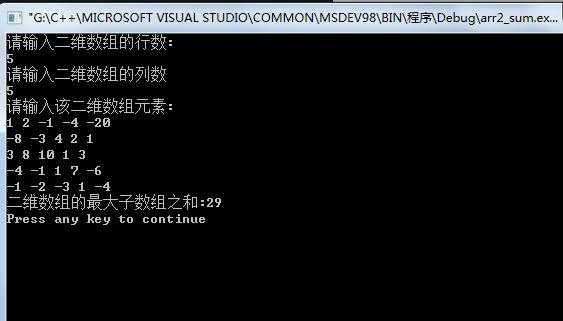
全正数时正确:
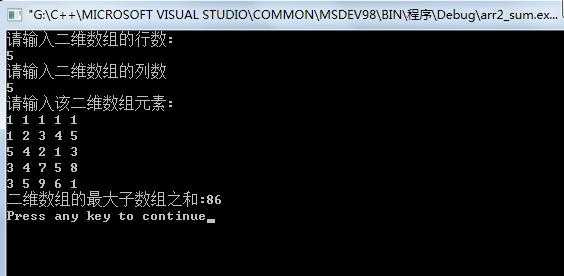
有正有负有零:
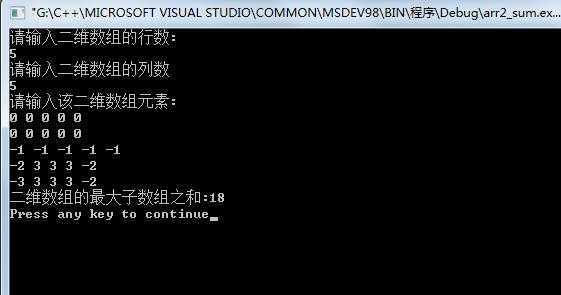
全负数时:
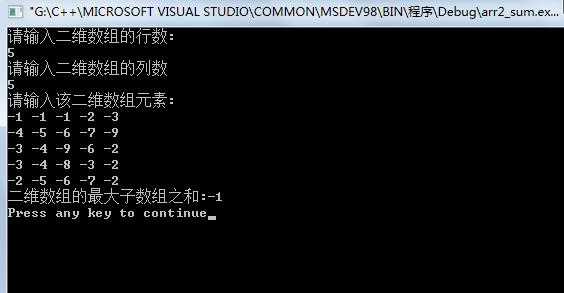
五、缺陷及总结:
本次结对我两在上次用动态法一维数组求最大子数组之和基础上,本次用穷举法先假设一数组元素P[i][j],之后求每个子数组之和并求其最大子数组之和即可,缺陷这样时间花费比较多。
六、工作合照:
待发
原文:http://www.cnblogs.com/2015tan/p/4361116.html