Lamda 表达式学习(2) ——lamda 变换

回顾λ-calculus语法：

t ::=  　　　　terms:

　　x  　　　　variable

　　λx.t  　　abstraction

　　t t  　　　application

λ-变换：保持λ-项含义的同时对其进行变换。

1. α-变换：改变被绑定变量的名称，所代表的含义仍是一样的。

λx.t → λy.t(x:=y)

(将表达式的body t中的所有x的自由出现替换称y)

两个lamda表达式如果可以通过α-变换（可能应用到子项）从一个变换到另外一个，则称他们是全等的。

2. β-规约：对application的变换，表示函数作用的概念。

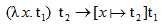
将t1中所有的自由的x替换为t2作为结果。

不允许任何beta归约的lambda表达式被称为Beta范式。不是所有的表达式都可以归约到范式。

3. η-变换：

Eta-conversion expresses the idea of extensionality, which in this context is that two functions are the same if and only if they give the same result for all arguments. Eta-conversion converts between λx.(f x) and f whenever x does not appear free in f.

Lamda 表达式学习(2) ——lamda 变换

原文：http://www.cnblogs.com/zhaohouhou/p/4354706.html