| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 7202 | Accepted: 4718 |
Description
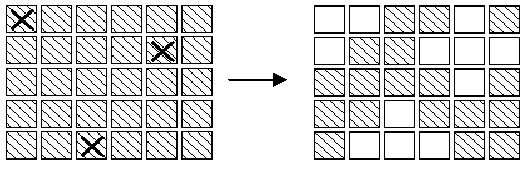
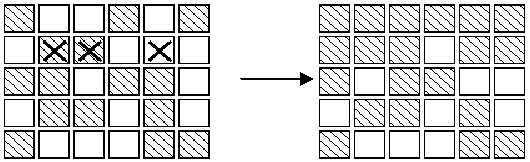
Input
Output
Sample Input
2 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0
Sample Output
PUZZLE #1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 PUZZLE #2 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1
分析来源:http://www.xuebuyuan.com/1394020.html
题意:有一个5*6的矩阵,每个位置都表示按钮和灯,1表示亮,0表示灭。每当按下一个位置的按钮,它和它周围灯的状态全部翻转,问在这样的一个方阵中按下哪些按钮可以把整个方阵都变成灭的,这时1表示按了,0表示没按。
以下分析部分转自:http://blog.csdn.net/shiren_Bod/article/details/5766907
这个游戏有一些技巧:
1、按按钮的顺序可以随便。
2、任何一个按钮都最多需要按下1次。因为按下第二次刚好抵消第一次,等于没有按。
这个问题可以转化成数学问题。
一个灯的布局可以看成一个0、1矩阵。以3x3为例:
0 1 0
1 1 0
0 1 1
表示一个布局。其中0表示灯灭,1表示灯亮。
每次按下按钮(POJ1222)或者叫一个宿舍关灯(0998),可以看成在原矩阵上加(模2加,就是按位异或)上一个如下的矩阵:
0 1 0
1 1 1
0 1 0
上述矩阵中的1表示按下第2行第2列的按钮时,作用的范围。如果按左上角的按钮,就是:
1 1 0
1 0 0
0 0 0
我们记L为待求解的原始布局矩阵。A(i,j)表示按下第i行第j列的按钮时的作用范围矩阵。在上述例子中,
L=
0 1 0
1 1 0
0 1 1
A(1,1)=
1 1 0
1 0 0
0 0 0
A(2,2)=
0 1 0
1 1 1
0 1 0
假设x(i,j)表示:想要使得L回到全灭状态,第i行第j列的按钮是否需要按下。0表示不按,1表示按下。那么,这个游戏就转化为如下方程的求解:
L + x(1,1)*A(1,1) + x(1,2)*A(1,2) + x(1,3)*A(1,3) + x(2,1)*A(2,1) + ... + x(3,3)*A(3,3) = 0
其中x(i,j)是未知数。方程右边的0表示零矩阵,表示全灭的状态。直观的理解就是:原来的L状态,经过了若干个A(i,j)的变换,最终变成0:全灭状态。
由于是0、1矩阵,上述方程也可以写成:
x(1,1)*A(1,1) + x(1,2)*A(1,2) + x(1,3)*A(1,3) + x(2,1)*A(2,1) + ... + x(3,3)*A(3,3) = L
这是一个矩阵方程。两个矩阵相等,充要条件是矩阵中每个元素都相等。将上述方程展开,便转化成了一个9元1次方程组:
简单地记做:AA * XX = LL
这个方程有唯一解:
x(1,1) x(1,2) x(1,3)
x(2,1) x(2,2) x(2,3)
x(3,1) x(3,2) x(3,3)
=
1 1 1
0 0 0
0 0 1
也就是说,按下第一行的3个按钮,和右下角的按钮,就
|
能使L状态变成全灭状态。
对于固定行列的阵列来说,AA矩阵也是确定的。是否存在解,解是否唯一,只与AA矩阵有关。对于唯一解的情形,只要将LL乘以AA的逆矩阵即可。具体求AA的逆矩阵的方法,可以用高斯消元法。 由于是0、1矩阵,上述方程也可以写成:
将1式两边同时加上一个L矩阵就可以变成 A(1,1)把矩阵 转化为一个列向量,L也转化为一个列向量, 将sigma xi*Ai=Li 对应位置的值相等就可以建立方程组了 X1*A(1,1)1+X2*A(1,2)1+X3*A(1,3)1+…………X30*A(30,30)1=L1; mod 2 X1*A(1,1)2+X2*A(1,2)2+X3*A(1,3)2+…………X30*A(30,30)2=L2; mod 2 X1*A(1,1)3+X2*A(1,2)3+X3*A(1,3)3+…………X30*A(30,30)3=L3 mod 2 ……. ……. ……. X1*A(1,1)30+X2*A(1,2)30+X3*A(1,3)30+…………X30*A(30,30)30=L30; mod 2 其中A(i,j)k 表示列向量A中第K个元素 这里的*表示点乘,Xi取(1,0) +表示模2加法,所以在高斯消元的时候可以用^异或运算 |
1个开关最多控制5个灯,在构造的矩阵中,a[i][j]=1表示第i个开关可以影响到j号灯
构造出的矩阵如图:
#include <iostream>
#include <cmath>
using namespace std;
int map[32][32];
int ans[32];
void Guass(){
for (int i=0;i<30;i++){ //控制行
if (map[i][i]==0){
for (int j=i+1;j<30;j++){ //找到不为0的那一行,然后进行交换
if (map[j][i]!=0){
for (int k=i;k<31;k++){
swap(map[j][k],map[i][k]);
}
break;
}
}
}
for (int j=0;j<30;j++){
if (i!=j&&map[j][i]){
for (int k=i;k<31;k++){
map[j][k]=map[i][k]^map[j][k];
}
}
}
}
for (int i=0;i<30;i++){
ans[i]=map[i][30];
}
}
int main(){
int t,kn,km,kx,ky;
cin>>t;
for (int cas=1;cas<=t;cas++){
for (int i=0;i<30;i++)
cin>>map[i][30];
for(int i=0;i<30;i++){ //构造30个方程
kn=i/6;
km=i%6;
for(int j=0;j<30;j++){
kx=j/6;
ky=j%6;
if(abs(kx-kn)+abs(ky-km)<=1)
map[i][j]=1;
else
map[i][j]=0;
}
}
Guass();
cout<<"PUZZLE #"<<cas<<endl;
for (int i=0;i<30;i++){
if ((i+1)%6==0)
cout<<ans[i]<<endl;
else
cout<<ans[i]<<" ";
}
}
return 0;
}原文:http://blog.csdn.net/codeforcer/article/details/43769171