思路分析:
二分查找法也称为折半查找法,它的思想是每次都与序列的中间元素进行比较。二分查找的一个前提条件是数组是有序的,假设数组array为递增序列,findData为要查找的数,n为数组长度,首先将n个元素分成个数大致相同的两半,取array[n/2]与将要查找的值findData进行比较,如果findData等于array[n/2],则找到findData,算法终止;如果findData<array[n/2],则只要在数组array的左半部分继续搜索findData;如果findData>array[n/2],则只需要在数组array的右半部分继续搜索即可。这个“左半部分”、“右半部分”的确定,都需要两个参数:开始标记与结束标记,比如初始状态时,开始标记为下标0,结束标记为数组长度-1,序列的中间元素下标就是开始标记+结束标记/2。要转到左半部分的中间元素,仅需要将结束标记改为中间元素下标-1;要转到右半部分的中间元素,则需要将开始标记改为中间元素下标+1。
切记,对于数组,无论是神马算法,操作之前的第一步一定是判断该数组是否存在,比如这样:
if(array==NULL||len<=0)
return -1;
对于非递归算法,自然是要用到循环了,在循环中开始标记和结束标记不断改变,循环的判断条件就是开始标记是否在结束标记之前。若查找成功则返回中间元素标记,若查找失败则返回-1。所以非递归算法需要三个参数:数组起始地址、数组长度以及要查找的数字。
对于递归算法,判断条件是一样的,在调用自身的过程中,要改变的参数要么是开始标记,要么是结束标记。所以对于递归算法,需要四个参数:数组起止地址、要查找的数字、开始标记与结束标记。
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 |
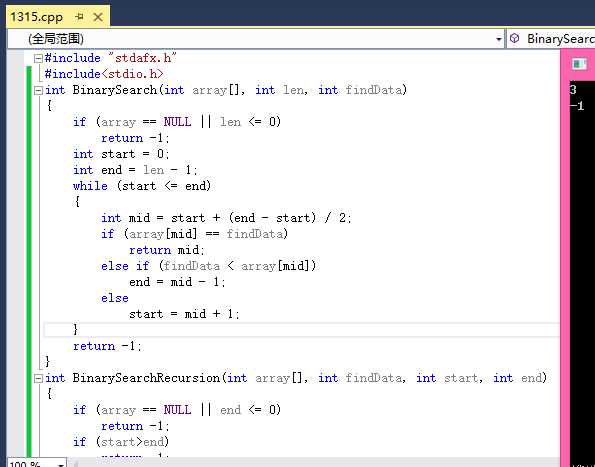
// 1315.cpp : 定义控制台应用程序的入口点。//#include "stdafx.h"#include<stdio.h>int BinarySearch(int
array[], int
len, int
findData){ if
(array == NULL || len <= 0) return
-1; int
start = 0; int
end = len - 1; while
(start <= end) { int
mid = start + (end - start) / 2; if
(array[mid] == findData) return
mid; else
if (findData < array[mid]) end = mid - 1; else start = mid + 1; } return
-1;}int
BinarySearchRecursion(int
array[], int
findData, int
start, int
end){ if
(array == NULL || end <= 0) return
-1; if
(start>end) return
-1; int
mid = start + (end - start) / 2; if
(array[mid] == findData) return
mid; else
if (findData < array[mid]) return
BinarySearchRecursion(array, findData, start, mid - 1); else return
BinarySearchRecursion(array, findData, mid + 1, end);}int
main(){ int
array[] = { 1, 2, 3, 4, 5, 6, 7, 8 }; int
len = sizeof(array) / sizeof(int); int
index = BinarySearch(array, len, 4); int
index2 = BinarySearchRecursion(array, 9,0,len); printf("%d\n%d\n", index, index2); getchar(); return
0;} |
效果如图:
如何分别使用递归与非递归实现二分查找算法,布布扣,bubuko.com
原文:http://www.cnblogs.com/cysolo/p/3585224.html