POJ 3744 Scout YYF I（矩阵快速幂 概率dp）

题目链接：http://poj.org/problem?id=3744

Description

Input

Output

Sample Input

1 0.5
2
2 0.5
2 4

Sample Output

0.5000000
0.2500000

题意： 

一共有n个雷，分别在a[1] a[2] ……a[n] ；

每次走一步概率为 p ，走两步概率为 1 - p ，起始位置在1号位置；

求能安全通过所有雷的概率；

PS：

把整个过程划分成阶段处理：

1 ~ a[1]

a[1]+1 ~ a[2]

…………

a[n-1]+1 ~ a[n]

那么只要求出每次踩到雷的概率，再求反面，最后把所有阶段的结果连乘就好了。

ans[i]表示踩中i的概率，推出： ans[i] = p*ans[i-1] + (1-p)*ans[i-2]

构造矩阵：

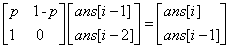
代码如下：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
struct Matrix
{
    double m[5][5];
} I, A;
double a[17];
//ans[i]表示猜到第i个地雷的概率
//ans[i] = p*ans[i-1] + (1-p)*ans[i-2];
const int ssize = 2;
Matrix Mul(Matrix a,Matrix b)
{
    int i, j, k;
    Matrix c;
    for(i = 1; i <= ssize; i++)
    {
        for(j = 1; j <= ssize; j++)
        {
            c.m[i][j]=0;
            for(k = 1; k <= ssize; k++)
            {
                c.m[i][j]+=(a.m[i][k]*b.m[k][j]);
//               c.m[i][j]%=mod;
            }
        }
    }
    return c;
}

Matrix quickpagow(int n)
{
    Matrix m = A, b = I;
    while(n)
    {
        if(n & 1)
            b = Mul(b,m);
        n = n >> 1;
        m = Mul(m,m);
    }
    return b;
}
double solve(int l, int r)
{
    if(l == r)
        return 1;
    if(r-l == 1)
        return 0;//相邻一定会踩到
    Matrix tt = quickpagow(r-l-1);
    return 1 - tt.m[1][1];//反面
}
int main()
{
    int n;
    double p;
    while(~scanf("%d%lf",&n,&p))
    {
        for(int i = 0; i < n; i++)
        {
            scanf("%lf",&a[i]);
        }
        sort(a,a+n);
        memset(A.m, 0,sizeof(A.m));
        memset(I.m, 0,sizeof(I.m));
        for(int i = 1; i <= ssize; i++)
        {
            I.m[i][i] = 1;
        }
        A.m[1][1] = p, A.m[1][2] = 1-p;
        A.m[2][1] = 1;
        double ans = solve(0,a[0]);
        for(int i = 1; i < n; i++)
        {
            ans *= solve(a[i-1],a[i]);
        }
        printf("%.7lf\n",ans);
    }
}

POJ 3744 Scout YYF I（矩阵快速幂 概率dp）

原文：http://blog.csdn.net/u012860063/article/details/43532221