在上篇博客中，我们提出了线性回归的概念，给出了一种使代价函数最小的方法：梯度下降法。在本篇博客中，我们给出另一种方法：正规方程。
是关于
的函数，要求此函数的最小值，有人说可以求导啊，另
，求出相应的
即可，本文提出的就是此方法。但是由于
是一个矩阵（向量是特殊的矩阵），我们需要关于矩阵求导方面的知识。
假设函数将
阶矩阵映射到实数空间，我们定义
对于
阶矩阵
求导为：
，
所以导函数也是阶的矩阵。例如假设：
，
而，求
:
另外介绍矩阵迹的概念：对于一个的矩阵
，它的迹就是它的对角线的元素求和：
，矩阵的迹有如下的性质：
上述介绍了矩阵函数的求导法则和矩阵迹的概念，下面给出一些后面要用到的结论：
大家不用太纠结于基础知识，只是一个推到工具而已，下面才是正题。磨好工具，就去砍柴吧：
我们的任务是对代价函数求导：即令，然后解出
。给定训练集，定义设计矩阵(design
matrix)
，其中
是输入特征的维数，
是训练集中训练样本的个数。将
写成下列形式：
同样，定义目标向量：
，由于，于是得到：
另外对于向量，我们有
，所以：
由
显然：
（1），
so：
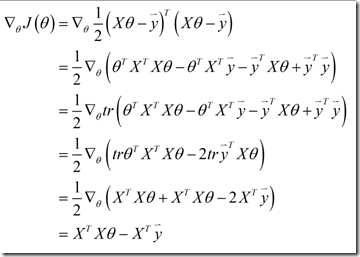注意在推导过程中，步骤4我们用到了公式（1），令。令导函数的值为0，我们得到正规方程：
解出：
好了，这就是我们要学习的。
总结一下：整篇充斥着公式推导，但思路很简单：欲求代价函数的最小值，令其导函数为0，求出参数即可。最后提点建议，机器学习中是有很多公式推倒的内容，本人认为结论固然重要，但得来的过程也很重要，只有知其然并知其所以然，才能对背后的思想有更深刻的认识。检验自己是否弄懂了公式：看自己能否独立推导出结果。
Linear Regression(线性回归)（二）—正规方程（normal equations）,布布扣,bubuko.com
Linear Regression(线性回归)（二）—正规方程（normal equations）
原文：http://www.cnblogs.com/hust-ghtao/p/3580188.html