[数学]矩阵总结

时间：2014-01-14 19:41:38 阅读：668 评论：0 收藏：0 [点我收藏+]

矩阵总结

By Wine93 2013.7

1.学习资料: 十个利用矩阵乘法解决的经典题目

2.矩阵最常见的5个作用

1. 求线性递推第n项 (POJ 3070 HDU 1757)

2. 已经线性递推式,求递推式中任意区间内的和,解这类题目有2种方法 (POJ 3233 非常经典的一题)

a) 递推式中的每一项相当于一个矩阵幂，求项和就相当于求矩阵幂和，而求矩阵幂和，又可以2分 (HDU 1588)

b) 在矩阵上加上一维记录和 S(n)=S(n-1)+f(n) 在求f(n)的时候顺便把s(n)也求出来了 (FZU 1683)

3. 对一系列数进行各种变换(加，减，乘，除，交换,异或，与等等....) (POJ 3735 HDU 2276)

4. 求a->b恰好走k步的的方案数 (HDU 2157)

5. 状态转移(灵活，设计好状态即可) (HDU 2604)

3.矩阵最常见的2个优化

1. 循环矩阵优化 (POJ 3150 HDU 2276)

循环矩阵：本行的每一项都是右上一行的每一项右移一个位置得到

Ex: 1 0 0 0 1

1 1 0 0 0

0 1 1 0 0

0 0 1 1 0

0 0 0 1 1

(如上，就是个循环矩阵)

根据循环矩阵的性质，循环矩阵乘以循环矩阵还是循环矩阵，所以我们在计算时，只要计算出第一行，就可以递推得到整个矩阵，所以可以将复杂度从O(n^3)降到O(n^2)

2. 无效元素(0元素)的去除 (POJ 3735)

在做题中会发现矩阵中出现大量的0元素，而这些元素在矩阵乘的时候是不发挥任何作用的，所以我们可以跳过这些0元素（通过改变乘的顺序）

4.经典例题选讲:

1.HDU 1757 A Simple Math Problem

http://acm.hdu.edu.cn/showproblem.php?pid=1757

题意：f(x)=x ( x<=10)

f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10) ( x>=10)

给出k,m,a0-a9,求出f(k)%m

分析：根据递推式构造矩阵即可

# include<cstdio>
# include<cstring>
# include<algorithm>
using namespace std;

# define LL long long
# define N 15
LL MOD;

struct Matrix 
{
    int n,m;
    LL a[N][N];
    void clear()
    {
        n=m=0;
        memset(a,0,sizeof(a));
    }
    
    Matrix operator *(const Matrix &b)const
    {
        Matrix res;
        res.clear();
        res.n=n,res.m=b.m;
        for(int i=0;i<n;i++)
            for(int j=0;j<b.m;j++)
                for(int k=0;k<m;k++)
                    res.a[i][j]=(res.a[i][j]+a[i][k]*b.a[k][j])%MOD;
        return res;
    }
};

Matrix PowMod(Matrix a,int n)
{
    Matrix res;
    res.clear();
    res.n=res.m=a.n;
    for(int i=0;i<res.n;i++)
        res.a[i][i]=1;
    while(n)
    {
        if(n&1)
            res=res*a;
        a=a*a;
        n>>=1;
    }
    return res;
}

int main()
{
    int n,i;
    Matrix a,b,res;
    while(scanf("%d %I64d",&n,&MOD)!=EOF)
    {
        b.n=10,b.m=1;
        for(i=0;i<10;i++)
            b.a[i][0]=i%MOD;
        a.clear();
        a.n=a.m=10;
        for(i=0;i<10;i++)
        {
            if(i!=9)
                a.a[i][i+1]=1;
            scanf("%d",&a.a[9][10-1-i]);
        }
        if(n<10)
            printf("%d\n",n%MOD);
        else
        {
            res=PowMod(a,n-9);
            res=res*b;
            printf("%I64d\n",res.a[9][0]);
        }
    }
    return 0;
}

HDU 1757

2.POJ 3233 Matrix Power Series

http://poj.org/problem?id=3233

题意：给出一个n*n的矩阵A,求S = A + A2 + A3 + … + Ak

分析：如k=6时

A + A^2 + A^3 + A^4 + A^5 + A^6 =(A + A^2 + A^3) + A^3*(A + A^2 + A^3)

二分求出前3项，再加上A^3 *(前3项)即可，而前3项又可以2分,不断2分求解 (Matrix 67博客中有详解)

# include<cstdio>
# include<cstring>
# include<algorithm>
using namespace std;

# define N 55
int MOD;

struct Matrix
{
    int n,m,a[N][N];
    void clear()
    {
        n=m=0;
        memset(a,0,sizeof(a));
    }
    
    Matrix operator +(const Matrix &b)const
    {
        Matrix res;
        res.n=n,res.m=m;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                res.a[i][j]=(a[i][j]+b.a[i][j])%MOD;
        return res;
    }
    
    Matrix operator *(const Matrix &b)const
    {
        Matrix res;
        res.clear();
        res.n=n,res.m=b.m;
        for(int i=0;i<n;i++)
            for(int j=0;j<b.m;j++)
                for(int k=0;k<m;k++)
                    res.a[i][j]=(res.a[i][j]+a[i][k]*b.a[k][j])%MOD;
        return res;
    }
    
};

Matrix PowMod(Matrix a,int n)
{
    int i,j;
    Matrix res;
    res.clear();
    res.n=res.m=a.n;
    for(i=0;i<res.n;i++)
        res.a[i][i]=1;
    while(n)
    {
        if(n&1)
            res=res*a;
        a=a*a;
        n>>=1;
    }
    return res;
}


Matrix pre(Matrix a,int k)
{
    Matrix tmp,res;
    if(k==1)
        return a;
    tmp=pre(a,k/2);
     res=tmp+PowMod(a,k/2)*tmp;
     if(k&1)
         res=res+PowMod(a,k);
    return res;
}

int main()
{
    int n,k,i,j;
    while(scanf("%d %d %d",&n,&k,&MOD)!=EOF)
    {
        Matrix a,res;
        a.clear();
        a.n=a.m=n;
        for(i=0;i<n;i++)
            for(j=0;j<n;j++)
                scanf("%d",&a.a[i][j]);
        res=pre(a,k);
        for(i=0;i<n;i++)
        {
            printf("%d",res.a[i][0]);
            for(j=1;j<n;j++)
                printf(" %d",res.a[i][j]);
            printf("\n");
        }
    }
    return 0;
}

POJ 3233

3.HDU 1588 Gauss Fibonacci

题意：给出k,b ,n,m;

g(i)=k*i+b, f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2) (n>=2) (f(n)为斐波那契数列)

求f(g(i)) (0<=i<n) 前n-1项和

分析:A代表斐波那契数列构造的矩阵，则A^n的右上角的数字则是第n项斐波那契数列, 则f(g[i])=A^g(i)=A^(k*i+b)

所以原题就转换成了A^b+A^(k+b)+A^(2k+b)+A^(3k+b)+……+A^((n-1)k+b)

将A^b提出，则上式等于A^b*(1+A^k+A^2k+A^3k+……+A^(n-1)k)=A^b*( (A^k)^0+ (A^k)^1+(A^k)^2+(A^k)^3+……+(A^k)^n-1)

而 (A^k)^0+ (A^k)^1+(A^k)^2+(A^k)^3+……+(A^k)^n-1 这个式子就是POJ 3233所涉及的经典的2分再2分，就可以求得,求出这个后，A^b乘以这个矩阵幂和，取其右上角元素即为答案

# include<cstdio>
# include<cstring>
# include<algorithm>
using namespace std;

# define LL long long
# define N 5
LL MOD;

struct Matrix 
{
    int n,m;
    LL a[N][N];
    void clear()
    {
        n=m=0;
        memset(a,0,sizeof(a));
    }
    
    Matrix operator *(const Matrix &b)const
    {
        int i,j,k;
        Matrix res;
        res.clear();
        res.n=n,res.m=b.m;
        for(i=0;i<n;i++)
            for(k=0;k<m;k++)
            {
                if(a[i][k]==0)
                    continue;
                for(j=0;j<b.m;j++)
                {
                    res.a[i][j]=res.a[i][j]+a[i][k]*b.a[k][j];
                    res.a[i][j]-=res.a[i][j]/MOD*MOD;
                }
            }
        return res;
    }
    
    Matrix operator +(const Matrix &b)const
    {
        Matrix res;
        res.n=n,res.m=m;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            {
                res.a[i][j]=a[i][j]+b.a[i][j];
                if(res.a[i][j]>=MOD)
                    res.a[i][j]-=MOD;
            }    
        return res;
    }
};

Matrix PowMod(Matrix a,LL n)
{
    Matrix res;
    res.clear();
    res.n=res.m=a.n;
    for(int i=0;i<res.n;i++)
        res.a[i][i]=1;
    while(n)
    {
        if(n&1)
            res=res*a;
        a=a*a;
        n>>=1;
    }
    return res;
}

Matrix pre(Matrix a,LL n)
{
    if(n==1)
        return a;
    Matrix tmp=pre(a,n/2);
    Matrix res=tmp+PowMod(a,n/2)*tmp;
    if(n&1)
        res=res+PowMod(a,n);
    return res;
}

int main()
{
    LL k,b,n;
    Matrix a,ab,ak,res;
    a.clear();
    a.n=a.m=2;
    a.a[0][1]=a.a[1][0]=a.a[1][1]=1;
    while(scanf("%I64d %I64d %I64d %I64d",&k,&b,&n,&MOD)!=EOF)
    {
        res.clear();
        res.n=res.m=2;
        res.a[0][0]=res.a[1][1]=1;
        ab=PowMod(a,b);
        ak=PowMod(a,k);
        if(n>=2)
            res=res+pre(ak,n-1);
        res=res*ab;
        printf("%I64d\n",res.a[0][1]);
    }
    return 0;
}

HDU 1588

4.FZU 1588 纪念SlingShot

http://acm.fzu.edu.cn/problem.php?pid=1683

题意：给出递推式 F（n）=3 * F（n-1）+2 * F（n-2）+7 * F（n-3），n>=3，

其中F（0）=1，F（1）=3，F（2）=5,求其前n项和MOD 2009

分析:因为S(n)=S(n-1)+f(n),所以我在在递推f(n)的时候也递推了S(n) ，构造如下矩阵

1 7 2 3 S(n-1) S(n-1)+7*f(n-3)+2*f(n-2)+3*f(n-1)

0 0 1 0 * f(n-3) = f(n-2)

0 0 0 1 f(n-2) f(n-1)

0 7 2 3 f(n-1) 7*f(n-3)+2*f(n-2)+3*f(n-1)

# include<cstdio>
# include<cstring>
# include<algorithm>
using namespace std;

# define LL long long
# define N 5
# define MOD 2009

struct Matrix 
{
    int n,m;
    int a[N][N];
    void clear()
    {
        n=m=0;
        memset(a,0,sizeof(a));
    }
    
    Matrix operator *(const Matrix &b)const
    {
        int i,j,k;
        Matrix res;
        res.clear();
        res.n=n,res.m=b.m;
        for(i=0;i<n;i++)
            for(k=0;k<m;k++)
            {
                if(a[i][k]==0)
                    continue;
                for(j=0;j<b.m;j++)
                {
                    res.a[i][j]=res.a[i][j]+a[i][k]*b.a[k][j];
                    res.a[i][j]-=res.a[i][j]/MOD*MOD;
                }
            }
        return res;
    }
    
    Matrix operator +(const Matrix &b)const
    {
        Matrix res;
        res.n=n,res.m=m;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            {
                res.a[i][j]=a[i][j]+b.a[i][j];
                if(res.a[i][j]>=MOD)
                    res.a[i][j]-=MOD;
            }    
        return res;
    }
};

Matrix PowMod(Matrix a,LL n)
{
    Matrix res;
    res.clear();
    res.n=res.m=a.n;
    for(int i=0;i<res.n;i++)
        res.a[i][i]=1;
    while(n)
    {
        if(n&1)
            res=res*a;
        a=a*a;
        n>>=1;
    }
    return res;
}

int main()
{
    LL n;
    int T,cas,i,ans;
    Matrix a,res;
    a.clear();
    a.n=a.m=4;
    a.a[0][0]=1,a.a[0][1]=7,a.a[0][2]=2,a.a[0][3]=3;
    a.a[1][2]=a.a[2][3]=1;
    a.a[3][1]=7,a.a[3][2]=2,a.a[3][3]=3;
    scanf("%d",&T);
    for(cas=1;cas<=T;cas++)
    {
        scanf("%I64d",&n);
        printf("Case %d: ",cas);
        if(n==0)
            printf("1\n");
        else if(n==1)
            printf("4\n");
        else if(n==2)
            printf("9\n");
        else
        {
            res=PowMod(a,n-2);
                    ans=res.a[0][0]*9+res.a[0][1]*1+res.a[0][2]*3+res.a[0][3]*5;
            ans-=ans/MOD*MOD;
            printf("%d\n",ans);
        }
    }
    return 0;
}

FZU 1588

5.HDU 2276 Kiki & Little Kiki 2

http://acm.hdu.edu.cn/showproblem.php?pid=2276

题意:给你一串字符串s(仅由01组成 0代表熄灭，1代表亮着)，代表strlen(s)个围成圈的电灯的状态,若当前灯泡的左边灯泡亮着，则改变当前灯泡的状态(0->1 1->0)

问经过n轮变换后每个灯泡的状态

分析:根据题目要求构建矩阵即可，就是对一系列数的变换，用异或代替+，与代替 *，构造出来的矩阵是循环矩阵，所以可以优化到O(n^2)

# include<cstdio>
# include<cstring>
# include<algorithm>
using namespace std;

# define N 105

struct Matrix
{
    int n,m,a[N][N];
    Matrix(int nn,int mm):n(nn),m(mm){};
    void clear() {memset(a,0,sizeof(a));}
    void E()
    {
        for(int i=0;i<n;i++)
            a[i][i]=1;
    }

    Matrix operator *(const Matrix &b)const
    {
        int i=0,j,k;
        Matrix res(n,b.m);
        for(j=0;j<b.m;j++)
        {
            res.a[i][j]=0;
            for(k=0;k<m;k++)
                res.a[i][j]^=(a[i][k]&b.a[k][j]);
        }
        for(i=1;i<n;i++)
        {
            res.a[i][0]=res.a[i-1][m-1];
            for(j=1;j<m;j++)
                res.a[i][j]=res.a[i-1][j-1];
        }
        return res;
    }
};

Matrix PowMod(Matrix a,int n)
{
    Matrix res(a.n,a.m);
    res.clear();
    res.E();
    while(n)
    {
        if(n&1)
            res=res*a;
        a=a*a;
        n>>=1;
    }
    return res;
}


int main()
{
    char s[105];
    int n,i,j,c,len;
    while(scanf("%d",&n)!=EOF)
    {
        scanf("%s",s);
        len=strlen(s);    
        Matrix a(len,len), b(len,1);
        a.clear();
        for(i=0;i<len;i++)
        {
            b.a[i][0]=s[i]-‘0‘;
            a.a[i][i]=1;
            if(i==0)
                a.a[0][len-1]=1;
            else
                a.a[i][i-1]=1;
        }
        Matrix res=PowMod(a,n);
        for(i=0;i<len;i++)
        {
            c=0;
            for(j=0;j<len;j++)
                c^=(res.a[i][j]&(s[j]-‘0‘));
            printf("%d",c);
        }
        printf("\n");
    }
    return 0;
}

HDU 2276

6.HDU 2157 How many ways??

http://acm.hdu.edu.cn/showproblem.php?pid=2157

题目：给你一些有向边,求从A到B恰好经过K步的方案数

分析：Matrix 67博客中有详细介绍，若a->b有边，则将矩阵中[a,b]设为1，经过K步就相当于求矩阵的K次幂

# include<cstdio>
# include<cstring>
# include<algorithm>
using namespace std;

# define N 25
# define MOD 1000

struct Matrix 
{
    int n,m;
    int a[N][N];
    void clear()
    {
        n=m=0;
        memset(a,0,sizeof(a));
    }
    
    Matrix operator *(const Matrix &b)const
    {
        Matrix res;
        res.clear();
        res.n=n,res.m=b.m;
        for(int i=0;i<n;i++)
            for(int j=0;j<b.m;j++)
                for(int k=0;k<m;k++)
                    res.a[i][j]=(res.a[i][j]+a[i][k]*b.a[k][j])%MOD;
        return res;
    }
};

Matrix PowMod(Matrix a,int n)
{
    Matrix res;
    res.clear();
    res.n=res.m=a.n;
    for(int i=0;i<res.n;i++)
        res.a[i][i]=1;
    while(n)
    {
        if(n&1)
            res=res*a;
        a=a*a;
        n>>=1;
    }
    return res;
}

int main()
{
    Matrix a,res;
    int i,n,m,u,v,T,k;
    while(scanf("%d%d",&n,&m)!=EOF&&(n+m))
    {
        a.clear();
        a.n=a.m=n;
        for(i=1;i<=m;i++)
        {
            scanf("%d%d",&u,&v);
            a.a[u][v]=1;
        }
        scanf("%d",&T);
        while(T--)
        {
            scanf("%d%d%d",&u,&v,&k);
            res=PowMod(a,k);
            printf("%d\n",res.a[u][v]);
        }
    }
    return 0;
}

HDU 2157

7. POJ 3420 Quad Tiling

http://poj.org/problem?id=3420

题意：用2*1的多米诺牌铺4*N 的地板，一共有多少种方案

分析:摘自matrix 67博客

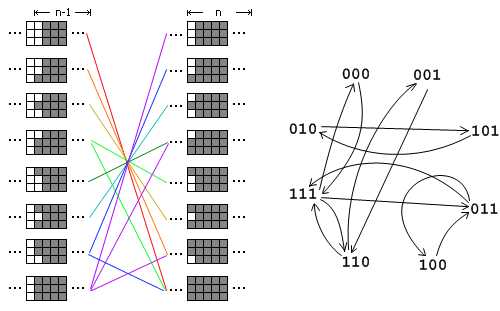
bubuko.com,布布扣

# include<cstdio>
# include<cstring>
# include<algorithm>
using namespace std;

# define N 55
# define LL long long
LL MOD;

struct Matrix
{
    int n,m;
    LL a[N][N];
    void clear()
    {
        n=m=0;
        memset(a,0,sizeof(a));
    }
    
    Matrix operator +(const Matrix &b)const
    {
        Matrix    res;
        res.n=n,res.m=m;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                res.a[i][j]=(a[i][j]+b.a[i][j])%MOD;
        return res;
    }
    
    Matrix operator -(const Matrix &b)const
    {
        Matrix res;
        res.n=n,res.m=m;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                res.a[i][j]=((a[i][j]-b.a[i][j])%MOD+MOD)%MOD;
        return res;
    }
    
    Matrix operator *(const Matrix &b)const
    {
        Matrix res;
        res.clear();
        res.n=n,res.m=b.m;
        for(int i=0;i<n;i++)
            for(int j=0;j<b.m;j++)
                for(int k=0;k<m;k++)
                    res.a[i][j]=(res.a[i][j]+a[i][k]*b.a[k][j])%MOD;
        return res;
    }
};


void build(Matrix &tmp)
{
    tmp.clear();
    tmp.n=tmp.m=16;
    for(int i=0;i<=7;i++)
        tmp.a[i][15-i]=tmp.a[15-i][i]=1;
    tmp.a[15][12]=tmp.a[12][15]=1;
    tmp.a[15][6]=tmp.a[6][15]=1;
    tmp.a[15][15]=tmp.a[15][15]=1;
    tmp.a[15][3]=tmp.a[3][15]=1;
}

int main()
{
    LL n;
    Matrix res,a;
    while(scanf("%I64d %I64d",&n,&MOD)!=EOF&&(n+MOD))
    {
        build(a);
        res.clear();
        res.n=res.m=16;
        for(int i=0;i<16;i++)
            res.a[i][i]=1;
        while(n)
        {
            if(n&1)
                res=res*a;
            a=a*a;
            n>>=1;
        }
        printf("%I64d\n",res.a[15][15]%MOD);
    }
    return 0;
}

POJ 3420

5.其余题目:

HDU 3483 A Very Simple Problem (构造十分巧妙)

HDU 2855 Fibonacci Check-up (构造十分巧妙)

HDU 4549 M斐波那契数列 (A^B%C=A^( B%phi(c)+phi(c)) %C B>=phi(c))

ZJU 2853 2974 3497 (历年浙江省省赛矩阵题，好题)

[数学]矩阵总结

原文：http://www.cnblogs.com/Wine93/p/3512684.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)