【题解】【直方图】【堆栈】【Codility】StoneWall

Cover "Manhattan skyline" using the minimum number of rectangles.

You are going to build a stone wall. The wall should be straight and N meters long, and its thickness should be constant; however, it should have different heights in different places. The height of the wall is specified by a zero-indexed array H of N positive integers. H[I] is the height of the wall from I to I+1 meters to the right of its left end. In particular, H[0] is the height of the wall‘s left end and H[N?1] is the height of the wall‘s right end.

The wall should be built of cuboid stone blocks (that is, all sides of such blocks are rectangular). Your task is to compute the minimum number of blocks needed to build the wall.

For example, given array H containing N = 9 integers:

 H[0] = 8 H[1] = 8 H[2] = 5 H[3] = 7 H[4] = 9 H[5] = 8 H[6] = 7 H[7] = 4 H[8] = 8 

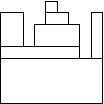
the function should return 7. The figure shows one possible arrangement of seven blocks.

Assume that:

• N is an integer within the range [1..100,000];
• each element of array H is an integer within the range [1..1,000,000,000].

Complexity:

• expected worst-case time complexity is O(N);
• expected worst-case space complexity is O(N), beyond input storage (not counting the storage required for input arguments).

Elements of input arrays can be modified.

思路：

其实Codility的叙述风格真的太啰嗦了，他们Solution还写得比较有趣，其实就是用的下图这种贪心算法，遍历数组遇到比栈顶小的就pop，横着切一刀分割出来一个矩形。

注意边界条件的先后顺序。

 1 #include <stack>
 2 int solution(const vector<int> &H) {
 3     int n = H.size();
 4     if(n <= 1) return n;
 5     int res = 0;
 6     stack<int> istack;
 7     for(int i = 0; i < n; i++){
 8         while(!istack.empty() && H[i] < istack.top()){
 9             istack.pop();
10             res++;
11         }
12         if(istack.empty()){
13             istack.push(H[i]);
14             continue;
15         }
16         if(H[i] > istack.top())
17             istack.push(H[i]);
18     }
19     res += istack.size();
20     return res;
21 }

【题解】【直方图】【堆栈】【Codility】StoneWall

原文：http://www.cnblogs.com/wei-li/p/StoneWall.html