| Time Limit: 12000MS | Memory Limit: 65536K | |
| Total Submissions: 2975 | Accepted: 1191 | |
| Case Time Limit: 2000MS | ||
Description
A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules that describe the new state of a cell based on the states of neighboring cells. Theorder of the cellular automaton is the number of cells it contains. Cells of the automaton of order n are numbered from 1 to n.
The order of the cell is the number of different values it may contain. Usually, values of a cell of order m are considered to be integer numbers from 0 to m ? 1.
One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. In this problem we examine the special kind of cellular automaton — circular cellular automaton of order n with cells of orderm. We will denote such kind of cellular automaton as n,m-automaton.
A distance between cells i and j in n,m-automaton is defined as min(|i ? j|, n ? |i ? j|). A d-environment of a cell is the set of cells at a distance not greater than d.
On each d-step values of all cells are simultaneously replaced by new values. The new value of cell i after d-step is computed as a sum of values of cells belonging to the d-enviroment of the cell i modulo m.
The following picture shows 1-step of the 5,3-automaton.
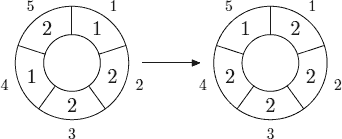
The problem is to calculate the state of the n,m-automaton after k d-steps.
Input
The first line of the input file contains four integer numbers n, m, d, and k (1 ≤ n ≤ 500, 1 ≤ m ≤ 1 000 000, 0 ≤ d < n?2 , 1 ≤ k ≤ 10 000 000). The second line contains n integer numbers from 0 to m ? 1 — initial values of the automaton’s cells.
Output
Output the values of the n,m-automaton’s cells after k d-steps.
Sample Input
sample input #1 5 3 1 1 1 2 2 1 2 sample input #2 5 3 1 10 1 2 2 1 2
Sample Output
sample output #1 2 2 2 2 1 sample output #2 2 0 0 2 2
Source
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define N 510
using namespace std;
__int64 a[N][N],b[N],temp[N][N];
int n,m,d,k;
int main()
{
//freopen("data.txt","r",stdin);
void f();
while(scanf("%d",&n)!=EOF)
{
scanf("%d %d %d",&m,&d,&k);
for(int i=0;i<=n-1;i++)
{
scanf("%I64d",&b[i]);
}
memset(a,0,sizeof(a));
for(int i=0;i<=n-1;i++)
{
for(int j=0;j<=d;j++)
{
int x = (i+j)%n;
a[i][x] = 1;
x = ((i-j)%n+n)%n;
a[i][x] = true;
}
}
f();
for(int i=0;i<=n-1;i++)
{
if(i==0)
{
printf("%I64d",b[i]);
}else
{
printf(" %I64d",b[i]);
}
}
printf("\n");
}
return 0;
}
void ba()
{
for(int i=0;i<=n-1;i++)
{
__int64 sum = 0;
for(int j=0;j<=n-1;j++)
{
sum=(sum+(b[j]*a[j][i])%m)%m;
}
temp[0][i] = sum;
}
for(int i=0;i<=n-1;i++)
{
b[i] = temp[0][i];
}
}
void aa()
{
for(int row=0;row<=0;row++)
{
for(int col=0;col<=n-1;col++)
{
__int64 sum = 0;
for(int i=0;i<=n-1;i++)
{
sum=(sum+(a[row][i]*a[i][col])%m)%m;
}
temp[row][col] = sum;
}
}
for(int i=0;i<=n-1;i++)
{
a[0][i] = temp[0][i];
}
int pian = 1;
for(int i=1;i<=n-1;i++)
{
for(int j=0;j<=n-1;j++)
{
int pos = (pian+j)%n;
a[i][pos] = a[0][j];
}
pian++;
}
}
void f()
{
while(k>1)
{
if(k&1)
{
ba();
}
aa();
k=k>>1;
}
ba();
}
原文:http://blog.csdn.net/yongxingao/article/details/19812827