目前为止,我们已经讨论神经网络在有监督学习中的应用。在有监督学习中,训练样本是有类别标签的。现在假设我们只有一个没有带标签的训练样本集合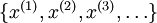 ,其中
,其中 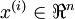 。自编码神经网络是一种无监督学习算法,它使用了反向传播算法,并让目标值等于输入值,比如
。自编码神经网络是一种无监督学习算法,它使用了反向传播算法,并让目标值等于输入值,比如 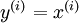 。下图是一个自编码神经网络的示例。
。下图是一个自编码神经网络的示例。
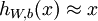 的函数。换句话说,它尝试逼近一个恒等函数,从而使得输出
的函数。换句话说,它尝试逼近一个恒等函数,从而使得输出 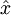 接近于输入
接近于输入  。恒等函数虽然看上去不太有学习的意义,但是当我们为自编码神经网络加入某些限制,比如限定隐藏神经元的数量,我们就可以从输入数据中发现一些有趣的结构。举例来说,假设某个自编码神经网络的输入x是一张10×10图像(共100个像素)的像素灰度值,于是n=100,其隐藏层
。恒等函数虽然看上去不太有学习的意义,但是当我们为自编码神经网络加入某些限制,比如限定隐藏神经元的数量,我们就可以从输入数据中发现一些有趣的结构。举例来说,假设某个自编码神经网络的输入x是一张10×10图像(共100个像素)的像素灰度值,于是n=100,其隐藏层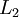 中有50个隐藏神经元,注意,输出也是100维的
中有50个隐藏神经元,注意,输出也是100维的 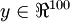 。由于只有50个隐藏神经元,我们迫使神经网络去学习输入数据的压缩表示,也就是说,它必须从50维的隐藏神经元激活度向量
。由于只有50个隐藏神经元,我们迫使神经网络去学习输入数据的压缩表示,也就是说,它必须从50维的隐藏神经元激活度向量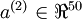 中重构出100维的像素灰度值输入
中重构出100维的像素灰度值输入  。如果网络的输入数据是完全随机的,比如每一个输入
。如果网络的输入数据是完全随机的,比如每一个输入
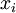 都是一个跟其它特征完全无关的独立同分布高斯随机变量,那么这一压缩表示将会非常难学习。但是如果输入数据中隐含着一些特定的结构,比如某些输入特征是彼此相关的,那么这一算法就可以发现输入数据中的这些相关性。事实上,这一简单的自编码神经网络通常可以学习出一个跟主元分析(PCA)结果非常相似的输入数据的低维表示。
都是一个跟其它特征完全无关的独立同分布高斯随机变量,那么这一压缩表示将会非常难学习。但是如果输入数据中隐含着一些特定的结构,比如某些输入特征是彼此相关的,那么这一算法就可以发现输入数据中的这些相关性。事实上,这一简单的自编码神经网络通常可以学习出一个跟主元分析(PCA)结果非常相似的输入数据的低维表示。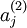 表示隐藏神经元j的激活度,但是这一表示方法中并未明确指出哪一个输入x带来了这一激活度。所以我们将使用
表示隐藏神经元j的激活度,但是这一表示方法中并未明确指出哪一个输入x带来了这一激活度。所以我们将使用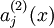 来表示在给定输入为x情况下,自编码神经网络隐藏神经元j的激活度。进一步,让
来表示在给定输入为x情况下,自编码神经网络隐藏神经元j的激活度。进一步,让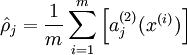
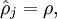
 是稀疏性参数,通常是一个接近于0的较小的值(比如
是稀疏性参数,通常是一个接近于0的较小的值(比如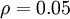 )换句话说,我们想要让隐藏神经元
)换句话说,我们想要让隐藏神经元  的平均活跃度接近0.05。为了满足这一条件,隐藏神经元的活跃度必须接近于0。
的平均活跃度接近0.05。为了满足这一条件,隐藏神经元的活跃度必须接近于0。 我们将会在我们的优化目标函数中加入一个额外的惩罚因子,而这一惩罚因子将惩罚那些  和
和  有显著不同的情况从而使得隐藏神经元的平均活跃度保持在较小范围内。惩罚因子的具体形式有很多种合理的选择,我们将会选择以下这一种:
有显著不同的情况从而使得隐藏神经元的平均活跃度保持在较小范围内。惩罚因子的具体形式有很多种合理的选择,我们将会选择以下这一种:
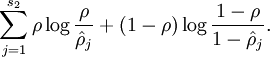
这里, 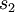 是隐藏层中隐藏神经元的数量,而索引
是隐藏层中隐藏神经元的数量,而索引  依次代表隐藏层中的每一个神经元。如果你对相对熵(KL
divergence)比较熟悉,这一惩罚因子实际上是基于它的。于是惩罚因子也可以被表示为
依次代表隐藏层中的每一个神经元。如果你对相对熵(KL
divergence)比较熟悉,这一惩罚因子实际上是基于它的。于是惩罚因子也可以被表示为
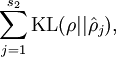
其中 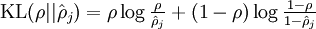 是一个以
是一个以  为均值和一个以
为均值和一个以  为均值的两个伯努利随机变量之间的相对熵。相对熵是一种标准的用来测量两个分布之间差异的方法。
为均值的两个伯努利随机变量之间的相对熵。相对熵是一种标准的用来测量两个分布之间差异的方法。
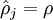 时
时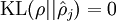 ,并且随着
,并且随着 与
与  之间的差异增大而单调递增。举例来说,在下图中,我们设定
之间的差异增大而单调递增。举例来说,在下图中,我们设定 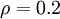 并且画出了相对熵值
并且画出了相对熵值 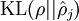 随着
随着  变化的变化。
变化的变化。
我们可以看出,相对熵在 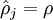 时达到它的最小值0,而当
时达到它的最小值0,而当  靠近0或者1的时候,相对熵则变得非常大(其实是趋向于
靠近0或者1的时候,相对熵则变得非常大(其实是趋向于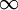 )。所以,最小化这一惩罚因子具有使得
)。所以,最小化这一惩罚因子具有使得  靠近
靠近  的效果。
现在,我们的总体代价函数可以表示为:
的效果。
现在,我们的总体代价函数可以表示为:
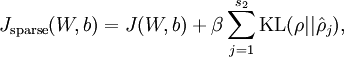
其中 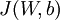 如之前所定义,而
如之前所定义,而 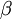 控制稀疏性惩罚因子的权重。
控制稀疏性惩罚因子的权重。 项则也(间接地)取决于
项则也(间接地)取决于 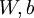 ,因为它是隐藏神经元
,因为它是隐藏神经元  的平均激活度,而隐藏层神经元的激活度取决于
的平均激活度,而隐藏层神经元的激活度取决于 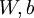 。
。
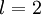 )更新的时候我们已经计算了
)更新的时候我们已经计算了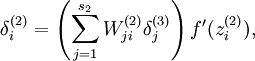
现在我们将其换成
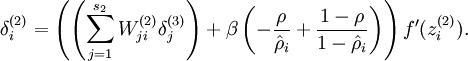
就可以了。
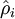 来计算这一项更新。所以在计算任何神经元的后向传播之前,你需要对所有的训练样本计算一遍前向传播,从而获取平均激活度。
来计算这一项更新。所以在计算任何神经元的后向传播之前,你需要对所有的训练样本计算一遍前向传播,从而获取平均激活度。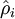 (当某一个前向传播的结果中的激活度
(当某一个前向传播的结果中的激活度 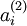 被用于计算平均激活度
被用于计算平均激活度 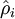 之后就可以将此结果删除)。然后当你完成平均激活度
之后就可以将此结果删除)。然后当你完成平均激活度 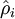 的计算之后,你需要重新对每一个训练样本做一次前向传播从而可以对其进行后向传播的计算。对于后一种情况,你对每一个训练样本需要计算两次前向传播,所以在计算上的效率会稍低一些。
的计算之后,你需要重新对每一个训练样本做一次前向传播从而可以对其进行后向传播的计算。对于后一种情况,你对每一个训练样本需要计算两次前向传播,所以在计算上的效率会稍低一些。
比如 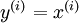 。下图是一个自编码神经网络的示例。
。下图是一个自编码神经网络的示例。
原文:http://www.cnblogs.com/rong86/p/3519094.html