How many ways

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。

如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)

点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

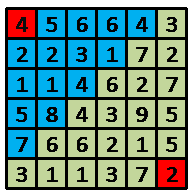
1
6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2

3948

这道题可以用如果用动态规划做，那就是初始化起始点方案数为1，每次枚举某一点能到达的位置，目标位置方案为能到达它的点方案数和。

如果是记忆化就是反过来做，终点位置方案数目为1，搜索过程记录搜到的每一点的方案数就好了。思路很清晰。

动态规划：

#include"stdio.h"
#include"string.h"
#define M 10000
#define N 110
int main()
{
    int T,i,j,n,m,x,y,di,dj,t;
    int a[N][N],dp[N][N];
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(i=1;i<=n;i++)
        {
            for(j=1;j<=m;j++)
            {
                scanf("%d",&a[i][j]);
            }
        }
        memset(dp,0,sizeof(dp));
        dp[1][1]=1;
        for(i=1;i<=n;i++)
        {
            for(j=1;j<=m;j++)
            {
                if(dp[i][j])
                {
                    t=a[i][j];
                    for(x=0;x<=t;x++)
                    {
                        for(y=0;y<=t;y++)
                        {
                            if(x+y==0)
                                continue;
                            if(x+y>t)
                                break;
                            di=x+i;
                            dj=y+j;
                            if(di<=n&&dj<=m)
                                dp[di][dj]+=dp[i][j];
                            dp[di][dj]%=M;
                        }
                    }
                }
            }
        }
        printf("%d\n",dp[n][m]%M);
    }    
    return 0;
}

记忆化搜索：

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
#define N 105
const int mod=10000;
int n,m;
int a[N][N];
int mark[N][N];
int dfs(int x,int y)
{
    if(mark[x][y]!=-1)
        return mark[x][y];
    int t,x1,y1,tmp;
    tmp=0;
    t=a[x][y];
    for(x1=0;x1<=t;x1++)
    {
        if(x+x1>=n)
            break;
        for(y1=0;x1+y1<=t;y1++)
        {
            if(y+y1>=m)
                break;
            if(x1+y1!=0)          //不能原地走
                tmp+=dfs(x+x1,y+y1);
        }
    }
    tmp%=mod;
    return mark[x][y]=tmp;
}
int main()
{
    int i,j,T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(i=0;i<n;i++)
        {
            for(j=0;j<m;j++)
            {
                scanf("%d",&a[i][j]);
                mark[i][j]=-1;
            }
        }
        mark[n-1][m-1]=1;
        printf("%d\n",dfs(0,0));
    }
    return 0;
}

hdu 1978 How many ways (动态规划、记忆化搜索)

原文：http://blog.csdn.net/u011721440/article/details/39576677