托勒密定理:圆内接四边形 \(ABCD\) 中 \(AB\cdot CD+ AD\cdot BC=AC\cdot BD\)。(证明截长补短即可)
中线定理:在 \(\triangle ABC\) 中,记 \(M\) 为 \(BC\) 边中点,则 \(AB^2+AC^2=\frac{1}{2}AM^2+BC^2\)。(证明使用向量)
Pappus 定理:
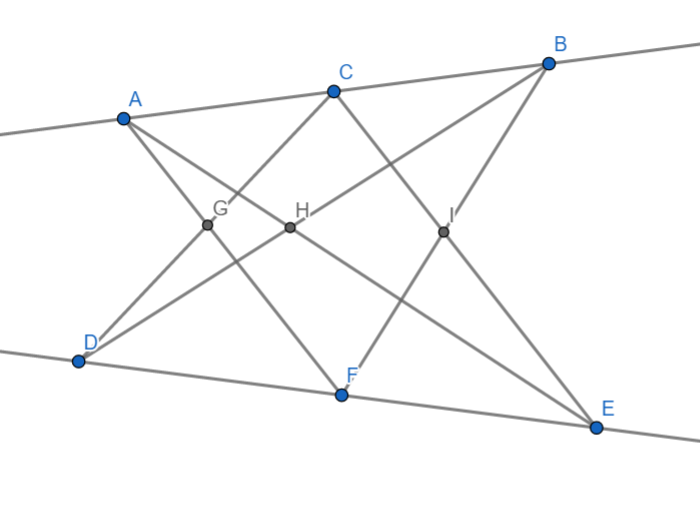
如图,\(GHI\) 三点共线。
Pascal 定理:
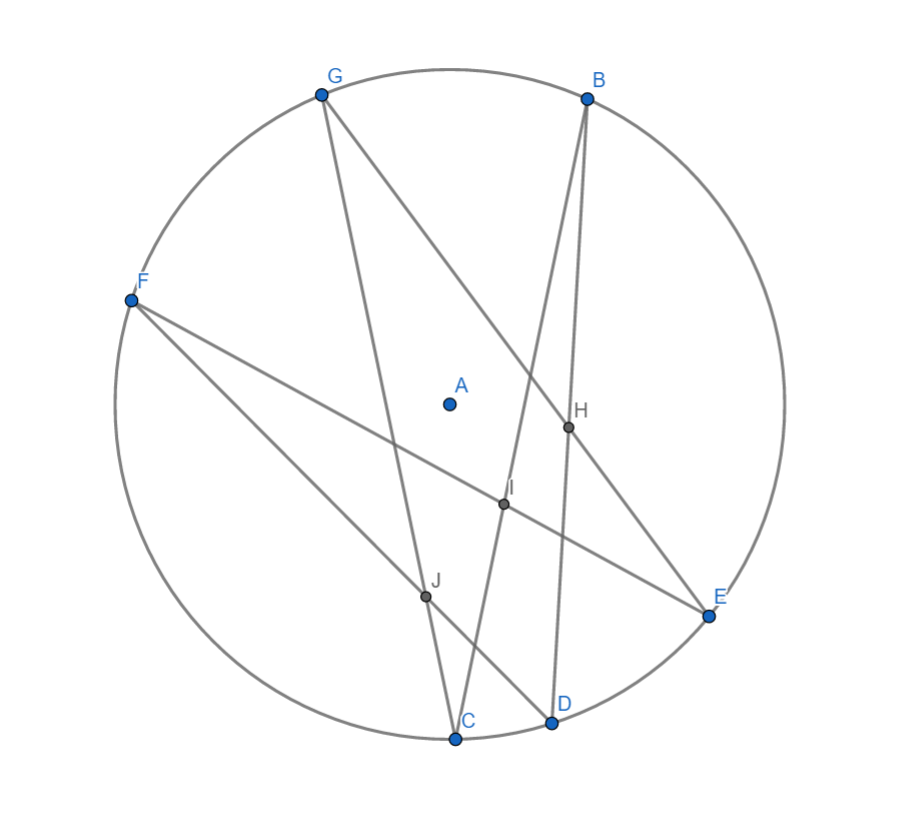
如图,圆内接六边形 \(BCGEFD\) 中,\(BC\cap EF=I\),\(CG\cap FD=J\),\(GE\cap BD=H\),\(HIJ\) 三点共线。
张角定理:在 \(\triangle ABC\) 中,\(D\) 是 \(BC\) 上的一点,则 \(\frac{\sin\angle BAD}{AC}+\frac{\sin\angle CAD}{AB}=\frac{\sin\angle BAC}{AD}\)。
原文:https://www.cnblogs.com/invisible-eyes/p/15187304.html