为什么前端计算不准确-number类型

什么是 number

js 中所有数字的默认类型都是number类型，number 对应Java等语言中的double类型，也就是64位的双精度浮点类型，即可以把number类型看作是一个double类型； js中还有一个类型 bigInt 表示任意大小的整数，与之对应Java等语言中的是BigInteger 表示任意大小的整数；

后台语言中还有BigDecimal类型表示任意大小浮点数 一般涉及到金额等需要精度较高时使用

了解64位的双精度浮点类型

1、64位代表什么

位的话很好理解，你的工资几位数啊，我工资8位数，位就是个数，工资8位数就是 用8个0~9的数字表示一个数值；我们这里的64位就是表示 64个二进制数，二进制 0 1，即number就是使用 64个0或者1来表示一个数；

扩展一下二进制知识，以byte类型（java中的类型 8位，不是指单位字节）为例：

   byte    类型   8位 
  第一个是符号位   0为正  1为负
  0111 1111  127      1111 1111  - 127                
  0000 0000  0  	    1000 0000  - 0 

  // +0、-0是没有意义的，把-0 表示-128 即最小负数的减一 （ -127 ）- 1 = -128 `
  // byte取值范围是[-128,127]
  // 这里的负数并不严谨，想仔细研究的需要看反码补码知识

二进制与十进制的相互转化

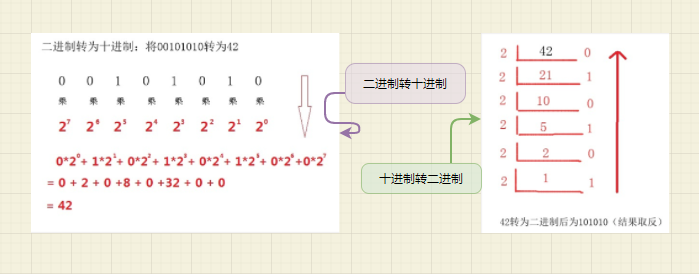整数的转化

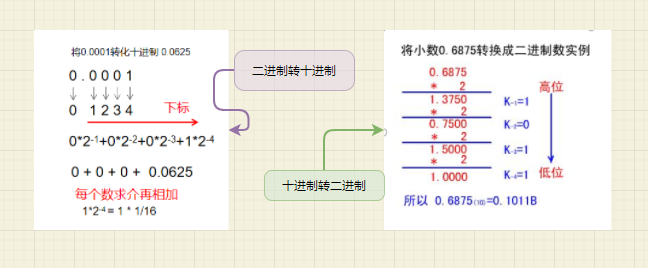小数的转化

0.1，0.2转二进制 ---> 结论（后面会说）：转成二进制后的数值本身就是一个近似值 不准确，0.2 与 0.1的不同是 小数点左移一位（乘以2）
0.1 0.0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 ...
0.2 0.0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 ...

2、什么是浮点数 ？

浮点数是一个组合 由一个 数字 乘以 基数 的 整数次幂 组成

浮点数类似科学计数法920000可以表示为9.2*10^5，读作9.2乘10的5次方

• 基数 一般就是我们的进制 十进制基数就是十 二进制基数就是二 固定的
• 数字（即尾数） 这里的数字也是我们说的有效数字
• 整数次幂 就是阶码 次方 阶码会改变会浮动

3、为什么要用浮点数 ？
这种设计可以在某个固定长度的存储空间内表示定点数无法表示的更大范围的数。如：五位数 不用科学计数法最大能表示 99999 ，使用科学计数法之后 9*10^9999,就能表示一个更大的数值；当然，阶数也不是越大越好，就像量身高的皮尺和写数学作业的三角尺，皮尺量的范围更大，但是不能很精确，皮尺最小单位就是厘米，所有厘米之后就只能靠猜测172.6cm、163.5cm ... ，但三角尺不一样最小单位毫米，就可以更精确的去计算；所有不能一味的之最求范围的大小还要考虑精度问题；

浮点数所能表示的范围取决于阶码；精度取决于尾数。

关于有效值：例如0.3065 小数部分左右段非0包起来的部分就是有效值，这里的有效值是3065，而小数-3.87：，387是有效值87是尾数。

阶数就是来控制我们小数点的位置的、 +1 变大(往右移动)、 -1 变小(往左移动)

介码特点

64位的双精度浮点类型的组成：1个符号位 表示正负，11个阶码表示范围，52个尾数有效数字表示精度

64位number组成

为什么最大安全数MAX_SAFE_INTEGER的取值是2^{53} - 1。有效数字不是52位吗？

64位number组成

• 【规格化】格式形成统一，浮点数通过调整阶码，写成小数点前不含有有效数字，小数点后第一位由非0数字表示，举例-306.5规格化为-0.3065*10^3 ；
• 二进制浮点数的规格化方法：通过调整小数点的阶码使得该数的有效值在1和2之间，既二进制浮点数的整数部分为1，例如：0.8125 = 0.1101（2） = 1.101*2（-1）；
• 因为有效数字的位数是被限制死的，而前导零（连续多个0 例如：0.0000012）会占用有效数字的空间，所以前导零越多有效数字越少，因此去除前导零才能保证有效数字位数的最大化。

number计算为什么不准确

我们都知道 0.1 +0.2 ！== 0.3 而是等于0.30000000000000004，为什么计算的结果会不准确呢

自己就是一个近似值
0.1 0.0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 ...

运算的过程中也会进行舍入值,浮点数的加减运算一般由，对介、尾数运算、规格化、舍入处理、溢出判断五个步骤，而这些步骤都是对结果取一个近似值；

1. 对介 对接就是对单位，12cm不能和1.52m直接加减，因为单位不同一个是厘米一个是米，所以需要把单位对齐0.12m和1.52m；对介的原则是小介对大介，即小单位变大单位，

例如：12cm，小介对大介变为米 小数点右移 结果等于 0.12m 但是长度不变，只能有两位数字，那么因为是右移所以2就会被舍弃，只能保留0.1m；否则大介对小介 1.52 变152cm 左移保留52，1会丢失，这样损失更大

2. 尾数运算 单位一样就可以相加减了
3. 规格化 做一定的取舍，保证运算得出的值也是一个符合规格化的值
4. 舍入处理 规格化之后，可能会添加或者舍去一些值，那些值将会保留起来，等到舍入处理时候需要把这些值做适当的加减，对原来的取舍进行补偿
5. 溢出判断 阶码也是可能超过范围的也需要检查是否溢出然后进行取舍

针对 计算不准确的解决办法

• toFixed(n) 保留n位小数 缺点：并不是四舍五入 不能直观的被我们掌控
• parseint（） 直接舍去小数 缺点：不能保留小数
• floor 下舍入、round四舍五入、ceil 上舍入 缺点：不能保留小数
• (a1000 + b1000) 缺点：不稳定不是所有的数都可以 例如：0.55 * 100 等于 55.00000000000001
• Math.round(X * 100) / 100 优点：指定小数尾数的四舍五入

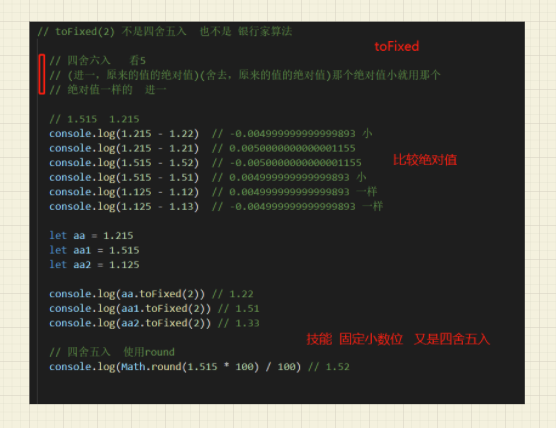toFixed的不同之处

为什么toFixed返回字符串

   1.0 *1  => 1
   Number(1.0)  => 1
  // 数值格式都会把 小数为0的自动省去
  // 所以 toFixed 要保存 1.00 格式的只能输出字符串

为什么前端计算不准确-number类型

原文：https://www.cnblogs.com/voxov/p/15181775.html