Kosaraju 算法

一.算法简介

在计算科学中，Kosaraju算法（又称为 Sharir Kosaraju算法 ）是一个线性时间(linear time) 算法, 用于找到的有向图的强连通分量。它利用了一个事实，逆图（与各边方向相同的图形反转, transpose graph）与原始图有相同的强连通分量。

逆图(Tranpose Graph )

我们对逆图定义如下：

若 \(G\) 为原始图, 则 \(G\) 的逆图 \(G^T\) 为

\(G^T=(V, E^T)\)，其中 \(E^T=\{(u, v):(v, u)∈E\}\)

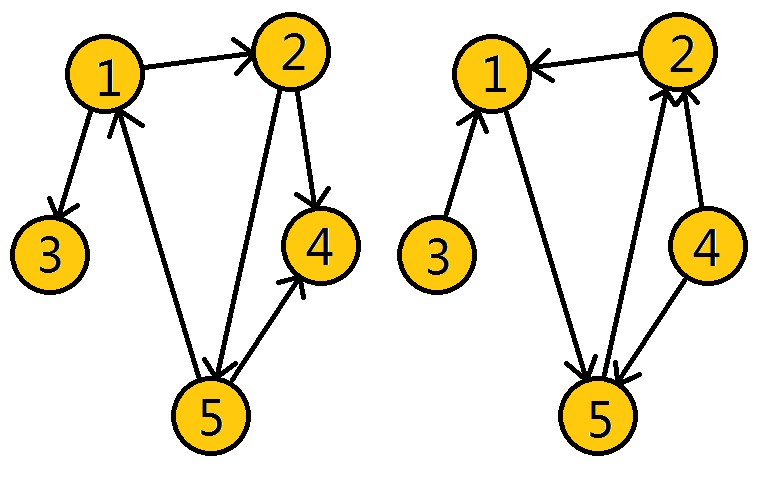
上图是有向图 \(G\) ， 和图 \(G\) 的逆图 \(G^T\)

通过以上的描述我们发现，Kosaraju 算法就是分别对原图 \(G\) 和它的逆图 \(G^T\) 进行两遍DFS，即：

1. .对原图 \(G\) 进行深度优先搜索，找出每个节点的完成时间(时间戳)

2. .选择完成时间较大的节点开始，对逆图 \(G^T\) 搜索，能够到达的点构成一个强连通分量

3. .如果 所有节点未都被遍历，重复2). ; 否则算法结束；

二.算法图示

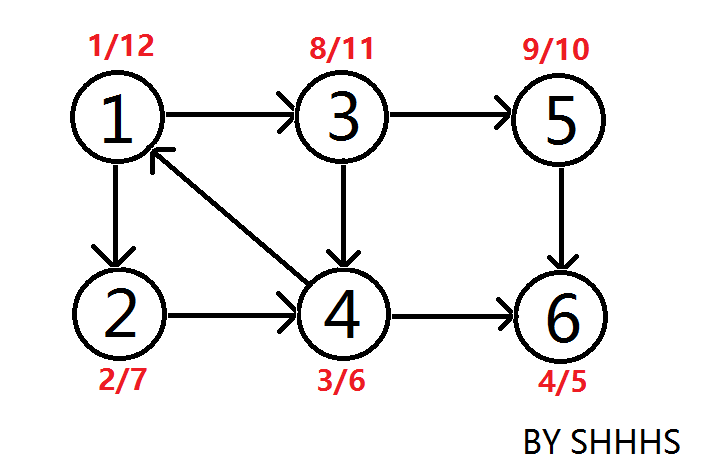
上图是对图 \(G\) ,进行一遍DFS的结果，每个节点有两个时间戳，即节点的发现时间 u.d 和 完成时间 u.f

我们按照 结束时间戳 由小到大 压入栈中

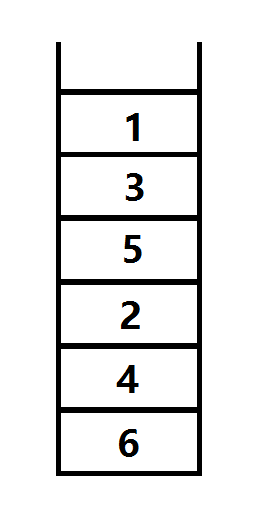
1. 每次从栈顶取出元素

2. 检查是否被访问过

3. 若没被访问过，以该点为起点，对逆图进行深度优先遍历

4. 否则返回第一步，直到栈空为止

[ATTENTION]

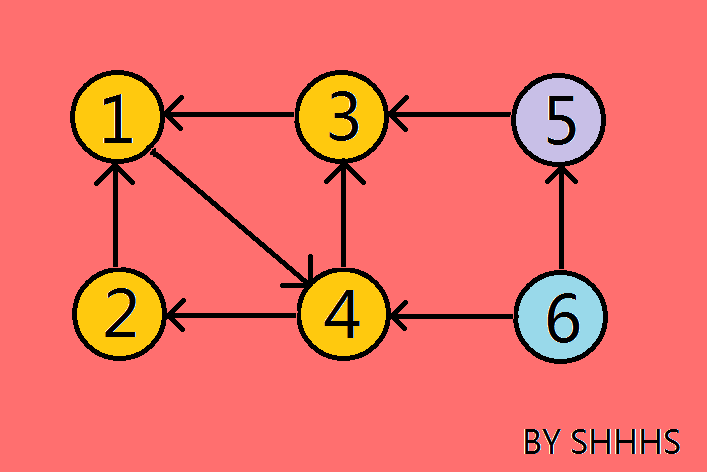
对逆图搜索时，从一个节点开始能搜索到的最大区块就是该点所在的强连通分量。

从节点1出发，能走到 2 ，3，4 ， 所以{1 , 2 , 3 , 4 }是一个强连通分量

从节点5出发，无路可走，所以{ 5 }是一个强连通分量

从节点6出发，无路可走，所以{ 6 }是一个强连通分量

自此Kosaraju Algorithm完毕，这个算法只需要两遍DFS即可，是一个比较易懂的求强连通分量的算法。

三.算法复杂度

• 邻接表：\(O(V+E)\)

• 邻接矩阵：\(O(V^2)\)

该算法在实际操作中要比Tarjan算法要慢

四.算法模板&注释代码

#include "cstdio"
#include "iostream"
#include "algorithm"

using namespace std;

const int maxN = 10010, maxM = 50010;

struct Kosaraju
{
    int to, next;
};

Kosaraju E[2][maxM];
bool vis[maxN];
int head[2][maxN], cnt[2], ord[maxN], sz[maxN], color[maxN];

int tot, dfs_num, col_num, N, M;

void Add_Edge(int x, int y, int _)
{ //建图
    E[_][++cnt[_]].to = y;
    E[_][cnt[_]].next = head[_][x];
    head[_][x] = cnt[_];
}

void DFS_1(int x, int _)
{
    dfs_num++; //发现时间
    vis[x] = true;
    for (int i = head[_][x]; i; i = E[_][i].next)
    {
        int temp = E[_][i].to;
        if (vis[temp] == false)
            DFS_1(temp, _);
    }
    ord[(N << 1) + 1 - (++dfs_num)] = x; //完成时间加入栈
}

void DFS_2(int x, int _)
{
    sz[tot]++; // 强连通分量的大小
    vis[x] = false;
    color[x] = col_num; //染色
    for (int i = head[_][x]; i; i = E[_][i].next)
    {
        int temp = E[_][i].to;
        if (vis[temp] == true)
            DFS_2(temp, _);
    }
}

int main()
{
    scanf("%d %d", &N, &M);
    for (int i = 1; i <= M; ++i)
    {
        int _x, _y;
        scanf("%d %d", &_x, &_y);
        Add_Edge(_x, _y, 0); //原图的邻接表
        Add_Edge(_y, _x, 1); //逆图的邻接表
    }
    for (int i = 1; i <= N; ++i)
        if (vis[i] == false)
            DFS_1(i, 0); //原图的DFS

    for (int i = 1; i <= (N << 1); ++i)
    {
        if (ord[i] != 0 && vis[ord[i]])
        {
            tot++;     //强连通分量的个数
            col_num++; //染色的颜色
            DFS_2(ord[i], 1);
        }
    }

    for (int i = 1; i <= tot; ++i)
        printf("%d ", sz[i]);
    putchar(‘\n‘);
    for (int i = 1; i <= N; ++i)
        printf("%d ", color[i]);
    return 0;
}

Kosaraju 算法

原文：https://www.cnblogs.com/syqwq/p/15145317.html