已经数表 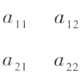
则表达式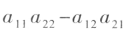 称为由数表所确定的二阶行列式,记作
称为由数表所确定的二阶行列式,记作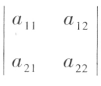
数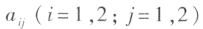 称为行列式的元素或元。元素的第一个下标 i 代表 行标,元素的第二个下标 j 代表 列标。
称为行列式的元素或元。元素的第一个下标 i 代表 行标,元素的第二个下标 j 代表 列标。
利用对角线法则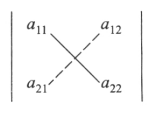 进行计算,实连线称为主对角线 ** ,虚连线称为副对角线**。
进行计算,实连线称为主对角线 ** ,虚连线称为副对角线**。
设有九个数字组成的三行三列数表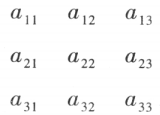
记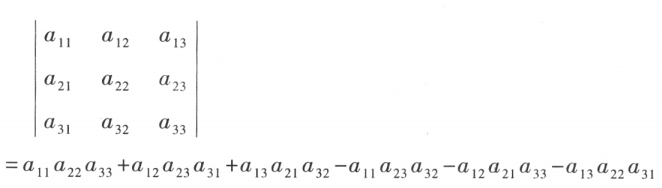
把 n 个不同的元素排成一列,叫做这 n 个元素的全排列。
对于 n 个不同的元素,先规定各元素之间有一个标准次序,在这 n 个元素的任一排列中,当某一对元素的先后次序与标准次序不同时,就说构成一个逆序。
一个排列中所有逆序的总数叫做这个排列的逆序数。
一个排列中的任意两个元素对换,排列改变奇偶性。
奇排列对换成标准排列的对换次数为奇数,偶排列对换成标准排列的对换次数为偶数。
设有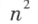 个数,排列成 n 行 n 列的数表
个数,排列成 n 行 n 列的数表
,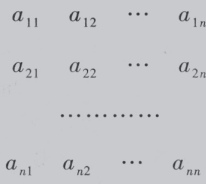
则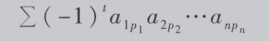
(t为这个排列的逆序数)称为 n 项行列式,
记作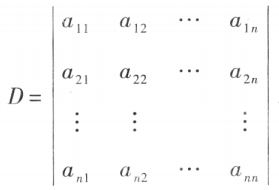
简记为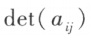 。
。
主对角线以上(以下)的元素都为 0 的行列式叫做上(下)三角形行列式。
主对角线以上和以下的元素都为 0 的行列式叫做对角行列式。
行列式与它的转置行列式相等。
即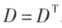
对换行列式的两行(列),行列式变号。
如果行列式有两行(列)完全相同,则此行列式等于零。
行列式的某一行(列)中所有的元素都乘同一数 k,等于用数 k 乘此行列式。
行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面。
行列式中如果有两行(列)元素成比例,则此行列式等于零。
若行列式的某一行(列)的元素都是两数之和,例如第 i 行的元素都是两数之和
,
把行列式的某一行(列)的各元素乘同一数然后加到另一行(列)对应的元素之上,行列式不变。
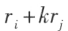 把行列式转化为上三角行列式。
把行列式转化为上三角行列式。在 n 阶行列式中,把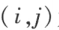 元
元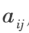 所在第 i 行和第 j 列划去后,留下来的 n-1 阶行列式叫做
所在第 i 行和第 j 列划去后,留下来的 n-1 阶行列式叫做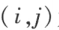 元
元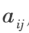 的余子式,记作
的余子式,记作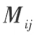
记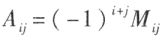 叫做
叫做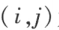 元
元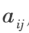 的代数余子式。
的代数余子式。
一个 n 阶行列式,如果其中第 i 行所有元素除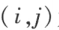 元
元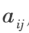 外都为零,那么这行列式等于
外都为零,那么这行列式等于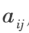 与它的代数余子式的乘积,
与它的代数余子式的乘积,
即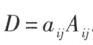
行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,
即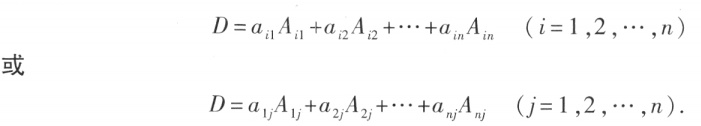
行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零,
即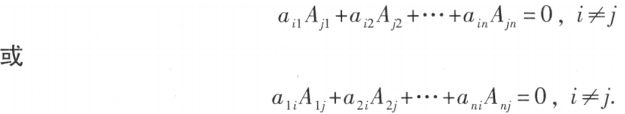
? **n **元非齐次线性方程,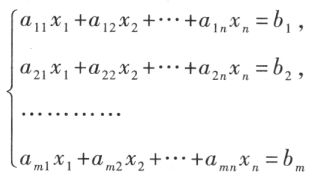
? n 元齐次线性方程,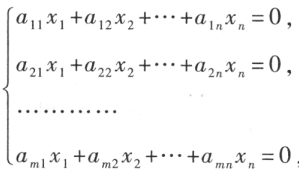
 的零解,但是不一定有非零解。
的零解,但是不一定有非零解。由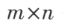 个数
个数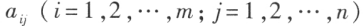 排成的 m 行 n 列的数表
排成的 m 行 n 列的数表
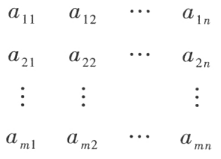
称为 m 行 n 列矩阵,简称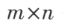 矩阵,
矩阵,
记作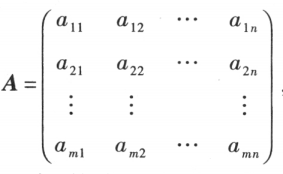
元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。
行数和列数都等于 n 的矩阵称为 n 阶矩阵或 n 阶方阵。
只有一行的矩阵
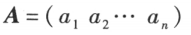
称为行矩阵,又称行向量。
只有一列的矩阵
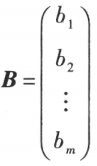
称为列矩阵,又称列向量。
两个矩阵的行数相等,列数也相等时,就称它们是同型矩阵。
元素都是零的矩阵称为零矩阵,记作 O。
注:不同型的零矩阵是不同的。
,
其中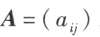 称为系数矩阵,
称为系数矩阵,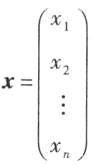 称为未知数矩阵,
称为未知数矩阵,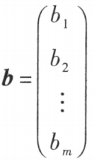 称为常数项矩阵,
称为常数项矩阵,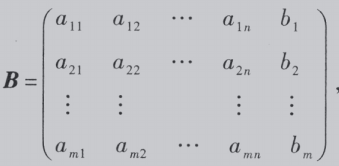 称为增广矩阵。
称为增广矩阵。
从左上角到右下角的直线(叫做对角线)以外的元素都是 0 ,这种方阵称为对角矩阵,简称对角阵,
记作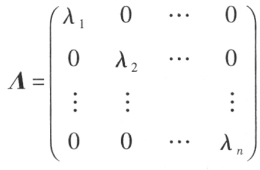 ,也记作
,也记作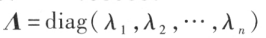
对角线上的元素都是 1 ,称为 n 阶单位矩阵,简称单位阵,
记作
设有两个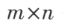 矩阵
矩阵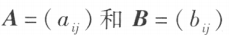 ,那么矩阵 A 与矩阵 B 的和记作 A + B,规定为
,那么矩阵 A 与矩阵 B 的和记作 A + B,规定为
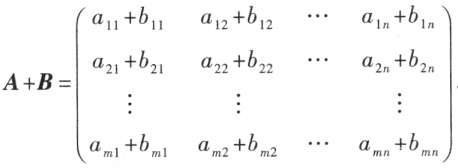
注意:只有当两个矩阵为同型矩阵时,这两个矩阵才能进行加法运算。
矩阵加法满足的规律: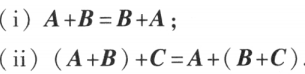
-A 称为 A 的负矩阵,有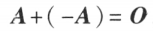
故矩阵的减法为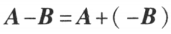
数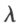 与矩阵 A 的乘积记作
与矩阵 A 的乘积记作 ,规定为
,规定为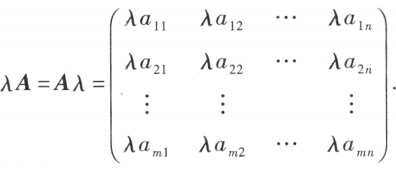
数乘矩阵满足的规律: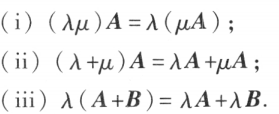
设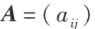 是一个
是一个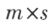 矩阵,
矩阵,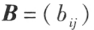 是一个
是一个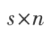 矩阵,那么规定矩阵 A 与矩阵 B 的乘积是一个
矩阵,那么规定矩阵 A 与矩阵 B 的乘积是一个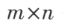 矩阵
矩阵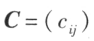 ,其中
,其中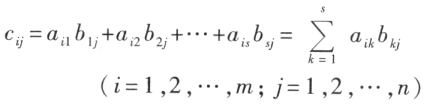
记作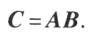
矩阵乘法注意事项:
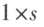 行矩阵与一个
行矩阵与一个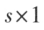 列矩阵的乘积是一个
列矩阵的乘积是一个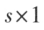 阶方阵,也就是一个数 。
阶方阵,也就是一个数 。矩阵乘法满足的规律: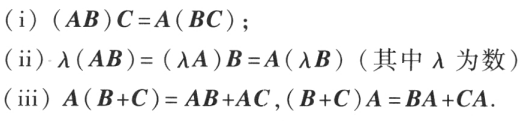
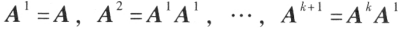
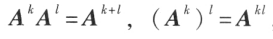
把矩阵 A 的行换成同序列数的列得到一个新矩阵,叫做 A 的转置矩阵,记作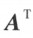
矩阵的转置满足的规律: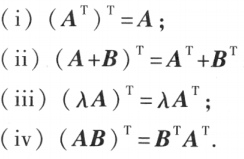
设 A 为 n 阶方阵,如果满足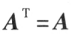 ,那么 A 称为对称矩阵,简称对称阵。
,那么 A 称为对称矩阵,简称对称阵。
由 n 阶方阵 A 的元素所构成的行列式(各元素的位置不变),称为方阵 A 的行列式,记作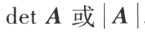 。
。
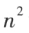 个数按一定方式排成的数表。
个数按一定方式排成的数表。由A确定的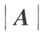 的这个运算满足下述运算规律:
的这个运算满足下述运算规律: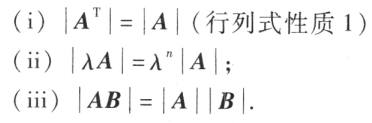
行列式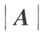 的各个元素的代数余子式
的各个元素的代数余子式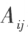 所构成的如下的矩阵称为 A 的伴随矩阵,简称伴矩阵。
所构成的如下的矩阵称为 A 的伴随矩阵,简称伴矩阵。
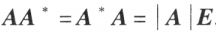
对于 n 阶矩阵 A,如果有一个 n 阶矩阵 B,使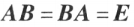 则说矩阵 A 是可逆的,并把矩阵 B 称为 A 的逆矩阵,简称逆阵,记作
则说矩阵 A 是可逆的,并把矩阵 B 称为 A 的逆矩阵,简称逆阵,记作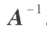 ,即若
,即若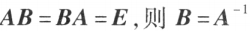
逆矩阵满足的运算规律:
若矩阵 A 可逆,则 。
。
若 ,则矩阵 A 可逆,且
,则矩阵 A 可逆,且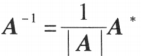
其中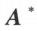 为矩阵 A 的伴随矩阵。
为矩阵 A 的伴随矩阵。
当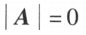 时,A 称为奇异矩阵,又称满秩矩阵,否则称非奇异矩阵。
时,A 称为奇异矩阵,又称满秩矩阵,否则称非奇异矩阵。
 ,即可逆矩阵就是非奇异矩阵,也称为降秩矩阵。
,即可逆矩阵就是非奇异矩阵,也称为降秩矩阵。若 ,则
,则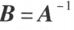
如果线性方程组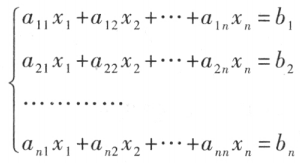 的系数矩阵 A 的行列式不等于零
的系数矩阵 A 的行列式不等于零
那么方程组有惟一解
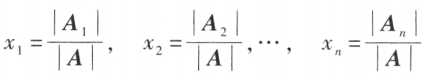
其中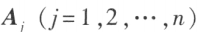 是把系数矩阵 A 中第 j 列的元素用方程组右端的常数项 代替后所得到的 n 阶矩阵,即
是把系数矩阵 A 中第 j 列的元素用方程组右端的常数项 代替后所得到的 n 阶矩阵,即
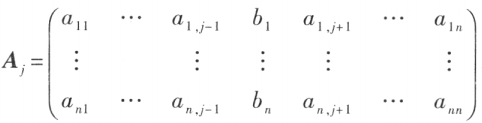
将矩阵 A 用若干条纵线和横线分成许多个小矩阵,每一个小矩阵称为 A 的子块,以子块元素的形式上的矩阵称为分块矩阵。
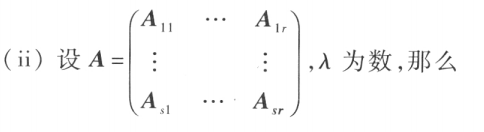
分块矩阵满足的规律:
,
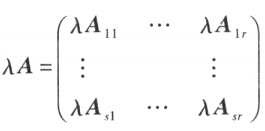
,
,
设 A 为 n 阶方阵,若 A 的分块矩阵只有在对角线上有非零子块,其余子块都为零矩阵,且在对角线上的子块都是方阵,其中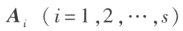 都是方阵,那么称 A 为分块对角矩阵。
都是方阵,那么称 A 为分块对角矩阵。
下面三种变换称为矩阵的初等行变换:
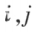 两行,记作
两行,记作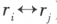
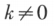 乘某一行中的所有元(第 i 行乘 k ,记作
乘某一行中的所有元(第 i 行乘 k ,记作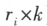 ;
;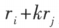 。
。如果矩阵 A 经有限次初等行变换变成矩阵 B,就称矩阵 A 与 B 行等价,记作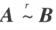
如果矩阵 A 经有限次初等列变换变成矩阵 B,就称矩阵 A 与 B 列等价,记作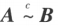
如果矩阵 A 经有限次初等变换变成矩阵 B,就称矩阵 A 与 B 等价,记作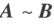
非零矩阵若满足
则称此矩阵为行阶梯形矩阵。
进一步,若 A 是行阶梯形矩阵,并满足:
则称A为行最简形矩阵。
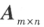 ,总可以经有限次初等行变换把它变为行阶梯形矩阵和最简形矩阵。
,总可以经有限次初等行变换把它变为行阶梯形矩阵和最简形矩阵。对行最简形矩阵再施以初等列变换,可变成一种形状更简单的矩阵,称为标准形。
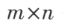 矩阵 A,总可经过初等变换(行变换和列变换)把它化为标准形
矩阵 A,总可经过初等变换(行变换和列变换)把它化为标准形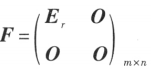 其中 r 就是行阶梯形矩阵中非零行的行数。
其中 r 就是行阶梯形矩阵中非零行的行数。设 A 与 B 为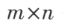 矩阵,那么
矩阵,那么
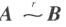 的充分必要条件是存在 m 阶可逆矩阵 P,使
的充分必要条件是存在 m 阶可逆矩阵 P,使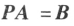 ;
;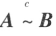 的充分必要条件是存在 n 阶可逆矩阵 Q,使
的充分必要条件是存在 n 阶可逆矩阵 Q,使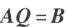 ;
;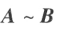 的充分必要条件使存在 m 阶可逆矩阵 P 以及 n 阶可逆矩阵 Q,使
的充分必要条件使存在 m 阶可逆矩阵 P 以及 n 阶可逆矩阵 Q,使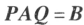
由单位矩阵E经过一次初等变换得到的矩阵称为初等矩阵。
设 A 是一个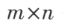 矩阵,对A施行一次初等行变换,相当于在 A 的左边乘相应的 m 阶初等矩阵;对 A 施行一次初等列变换,相当于在 A 的右边乘相应的 n 阶初等矩阵。
矩阵,对A施行一次初等行变换,相当于在 A 的左边乘相应的 m 阶初等矩阵;对 A 施行一次初等列变换,相当于在 A 的右边乘相应的 n 阶初等矩阵。
初等矩阵都是可逆的,且其逆矩阵是同一类型的初等矩阵:
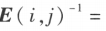
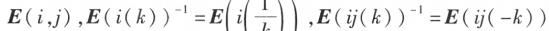
方阵 A 可逆的充分必要条件是存在有限个初等矩阵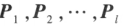 ,使
,使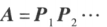
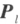
方阵 A 可逆的充分必要条件使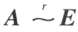
在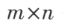 矩阵 A 中,任取 k 行与 k 列
矩阵 A 中,任取 k 行与 k 列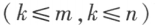 ,位于这些行列交叉处的
,位于这些行列交叉处的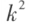 个元素,不改变它们在 A 中所处的位置次序而得的 k 阶行列式,称为 A 的 k 阶子式。
个元素,不改变它们在 A 中所处的位置次序而得的 k 阶行列式,称为 A 的 k 阶子式。
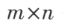 矩阵A的 k 阶子式共有
矩阵A的 k 阶子式共有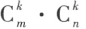 个。
个。设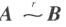 ,则 **A **与 B 中非零子式的最高阶数相同。
,则 **A **与 B 中非零子式的最高阶数相同。
设在矩阵 A 中有一个不等于零的 r 阶子式 D,且所有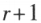 阶子式(如果存在的话)全等于零,那么 D 称为矩阵 A 的最高阶非零子式,数 r 称为矩阵的秩,记作
阶子式(如果存在的话)全等于零,那么 D 称为矩阵 A 的最高阶非零子式,数 r 称为矩阵的秩,记作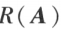 。
。
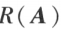 就是 A 的非零子式的最高阶数。
就是 A 的非零子式的最高阶数。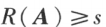 ,若 A 中所有 t 阶子式全为 0,则
,若 A 中所有 t 阶子式全为 0,则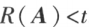
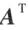 的子式与 A 的子式对应相等,从而
的子式与 A 的子式对应相等,从而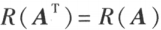
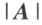 ,故当
,故当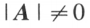 时
时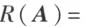
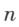 ,当
,当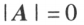 时
时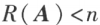 .可见可逆矩阵的秩等于矩阵的阶数,不可逆矩阵的秩小于矩阵的阶数。
.可见可逆矩阵的秩等于矩阵的阶数,不可逆矩阵的秩小于矩阵的阶数。若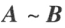 ,则
,则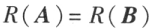
若可逆矩阵P、Q使 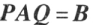 ,则
,则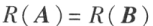
矩阵秩基本性质:
常用性质:
矩阵 A 的秩等于它的列数,这样的矩阵叫做列满秩矩阵。当 A 为方阵时,列满秩矩阵就成为满秩矩阵,也就是可逆矩阵。
设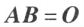 ,若A为列满秩矩阵,则
,若A为列满秩矩阵,则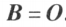
n 元线性方程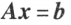
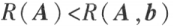
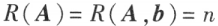
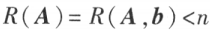
n 元齐次线性方程组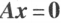 有非零解的充分必要条件是
有非零解的充分必要条件是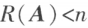
线性方程组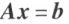 有解的充分必要条件是
有解的充分必要条件是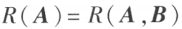
矩阵方程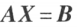 有解的充分必要条件是
有解的充分必要条件是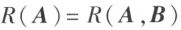
n 个有次序的数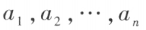 所组成的数组称为 n 维向量,这 n 个数称为该向量的 n 个分量,第 i 个数
所组成的数组称为 n 维向量,这 n 个数称为该向量的 n 个分量,第 i 个数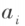 称为第 i 个分量。
称为第 i 个分量。
若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组。
给定向量组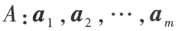 ,对于任一组实数
,对于任一组实数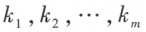 ,表达式
,表达式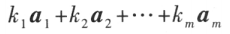 称为向量组A 的一个线性组合,
称为向量组A 的一个线性组合,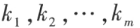 称为线性组合的系数。
称为线性组合的系数。
向量 b 能由向量组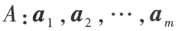 线性表示的充分必要条件是矩阵
线性表示的充分必要条件是矩阵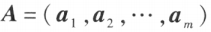 的秩等于矩阵
的秩等于矩阵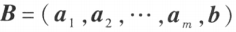 的秩。
的秩。
设有两个向量组: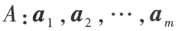 及
及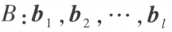 ,若 B 组中的每个向量都能由向量组 A 线性表示,则称向量组 B 能由向量组 A 线性表示。若向量组 A 与向量组 B 能相互线性表示,则称这两个向量组等价。
,若 B 组中的每个向量都能由向量组 A 线性表示,则称向量组 B 能由向量组 A 线性表示。若向量组 A 与向量组 B 能相互线性表示,则称这两个向量组等价。
向量组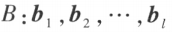 能由向量组
能由向量组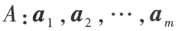 线性表示的充分必要条件是矩阵
线性表示的充分必要条件是矩阵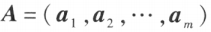 的秩等于矩阵
的秩等于矩阵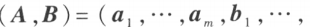
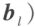 的秩,即
的秩,即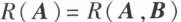
向量组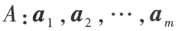 与向量组
与向量组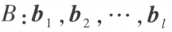 等价的充分必要条件是
等价的充分必要条件是
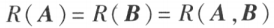
其中 A 和 B 是向量组 A 和 B 所构成的矩阵。
向量组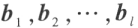 能由向量组
能由向量组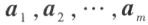 线性表示的充分必要条件是
线性表示的充分必要条件是
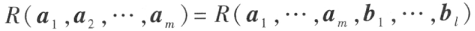
设向量组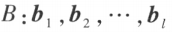 能由向量组
能由向量组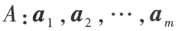 线性表示,
线性表示,
则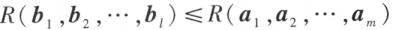
若向量组 B 能由向量组 A 线性表示,则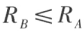
给定向量组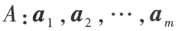 ,如果存在不全为零的数
,如果存在不全为零的数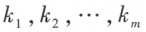 ,使
,使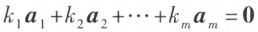 ,则称向量组 A 是线性相关的,否则称它线性无关。
,则称向量组 A 是线性相关的,否则称它线性无关。
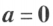 时是线性相关的,当
时是线性相关的,当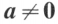 时是线性无关的。
时是线性无关的。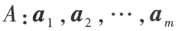 线性相关,则向量组
线性相关,则向量组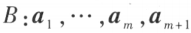 也线性相关。反之,若向量组B线性无关,则向量组A线性无关。
也线性相关。反之,若向量组B线性无关,则向量组A线性无关。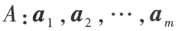 线性无关,而向量组
线性无关,而向量组 线性相关,则向量 b 必能由向量组 A 线性表示,且表示式时惟一的。
线性相关,则向量 b 必能由向量组 A 线性表示,且表示式时惟一的。设有向量组 A,如果在 A 中能选出 r 个向量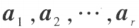 ,满足
,满足
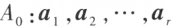 线性无关;
线性无关;那么称向量组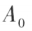 是向量组 A 的一个最大线性无关向量组(简称最大无关组),最大无关组所含向量个数r称为向量组A的秩,记作
是向量组 A 的一个最大线性无关向量组(简称最大无关组),最大无关组所含向量个数r称为向量组A的秩,记作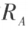
设向量组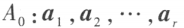 是向量组 A 的一个部分组,且满足
是向量组 A 的一个部分组,且满足
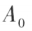 线性无关;
线性无关;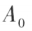 线性表示,
线性表示,那么向量组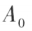 便是向量组A的一个最大无关组。
便是向量组A的一个最大无关组。
矩阵的秩等于它的列向量的秩,也等于它的行向量的秩。
若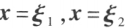 为为向量方程
为为向量方程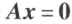 的解,则
的解,则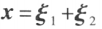 也是方程的解。
也是方程的解。
若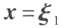 为向量方程
为向量方程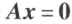 的解,k 为实数,则
的解,k 为实数,则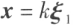 也是向量方程的解。
也是向量方程的解。
齐次线性方程组的解集的最大无关组称为该齐次线性方程的基础解系。
设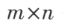 矩阵A的秩
矩阵A的秩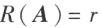 ,则 n 元齐次线性方程组
,则 n 元齐次线性方程组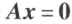 的解集 S 的秩
的解集 S 的秩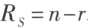
设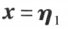 及
及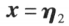 都是线性方程
都是线性方程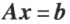 的解,则
的解,则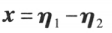 为对应的齐次线性方程组
为对应的齐次线性方程组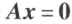 的解。
的解。
设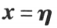 是方程
是方程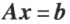 的解,
的解,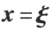 是方程
是方程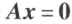 的解,则
的解,则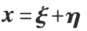 仍是方程
仍是方程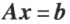 的解。
的解。
非齐次方程的通解 = 对应的齐次方程的通解 + 非齐次方程的一个特解 。
设 V 为 n 维向量的集合,如果集合 V 非空,且集合 V 对于向量的加法及数乘两种运算封闭,那么就称集合 V 为向量空间。
n 元齐次线性方程组的解集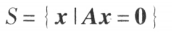
是一个向量空间(称为齐次线性方程组的解空间)。
设有向量空间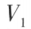 及
及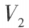 ,若
,若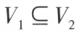 ,就称
,就称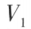 是
是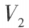 的子空间。
的子空间。
设 V 为向量空间,如果 r 个向量 ,且满足
,且满足
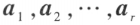 线性无关;
线性无关;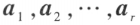 线性表示,
线性表示,那么,向量组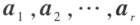 就称为向量空间 V 的一个基,r 称为向量空间 V 的维数,并称 V 为 r 维向量空间。
就称为向量空间 V 的一个基,r 称为向量空间 V 的维数,并称 V 为 r 维向量空间。
如果在向量空间 V 中取定一个基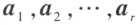 ,那么 V 中任一向量 x 可惟一地表示为
,那么 V 中任一向量 x 可惟一地表示为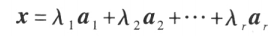 数组
数组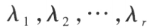 称为向量 x 在基
称为向量 x 在基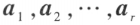 中的坐标。
中的坐标。
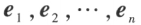 叫做向量空间
叫做向量空间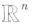 中的自然基。
中的自然基。设有 n 维向量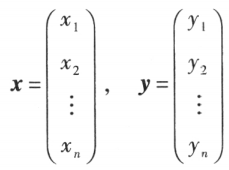 令
令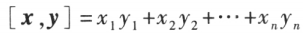 ,
,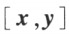 称为向量 x 与 y 的内积。
称为向量 x 与 y 的内积。
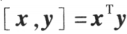
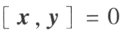 时,称向量 x 与 y 正交。
时,称向量 x 与 y 正交。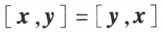 ;
;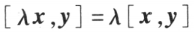 ;
;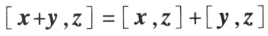 ;
;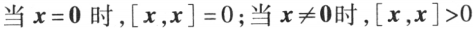 ;
;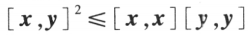
令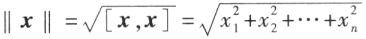 ,
,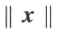 称为 n 维向量 x 的长度(或范数)。
称为 n 维向量 x 的长度(或范数)。
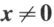 时,
时,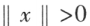 ;当
;当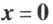 时,
时,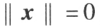 ;
;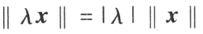 ;
;当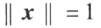 时,称为单位向量。
时,称为单位向量。
若 n 维向量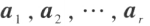 是一组两两正交的非零向量,则
是一组两两正交的非零向量,则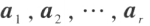 线性无关。
线性无关。
设 n 维向量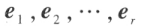 是向量空间
是向量空间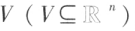 的一个基,如果
的一个基,如果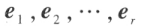 两两正交,且都是单位向量,则称
两两正交,且都是单位向量,则称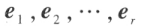 是
是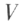 的一个标准正交基。
的一个标准正交基。

上述从线性无关向量组 导出正交向量组
导出正交向量组 的过程称为施密特正交化。
的过程称为施密特正交化。
如果 n 阶矩阵 A 满足 ,那么称 A 为正交矩阵,简称正矩阵。
,那么称 A 为正交矩阵,简称正矩阵。
正交矩阵有以下性质:
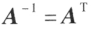 也是正交矩阵,且
也是正交矩阵,且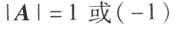 ;
;若 P 为正交矩阵,则线性变换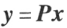 称为正交变换。
称为正交变换。
设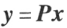 为正交变换,则有
为正交变换,则有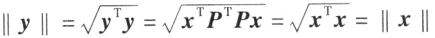 ,由于
,由于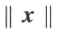 表示向量的长度,相当于线段的长度,因此
表示向量的长度,相当于线段的长度,因此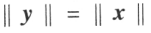
说明经过正交变换线段长度保持不变(从而三角形形状保持不变)。
设 A 是 n 阶矩阵,如果数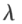 和 n 维非零列向量 x 使关系式
和 n 维非零列向量 x 使关系式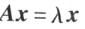 成立,那么,这样的数
成立,那么,这样的数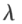 称为矩阵 A 的特征值,非零向量 x 称为 A 的对应于特征值
称为矩阵 A 的特征值,非零向量 x 称为 A 的对应于特征值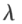 的特征向量。关系式也可写成
的特征向量。关系式也可写成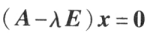 ,这是个未知数 n 个方程大的齐次线性方程组,它有非零解的充分必要条件使系数行列式
,这是个未知数 n 个方程大的齐次线性方程组,它有非零解的充分必要条件使系数行列式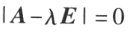 ,
,
即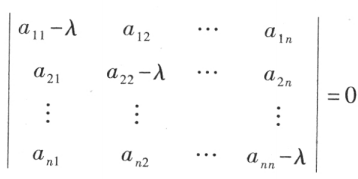
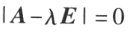 为A的特征方程,
为A的特征方程,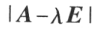 称为 A 的特征多项式,显然 A 的特征值就是特征方程的解。
称为 A 的特征多项式,显然 A 的特征值就是特征方程的解。设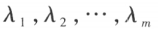 使方阵 A 的 m 个特征值,
使方阵 A 的 m 个特征值,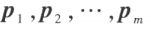 依次是与之对应的特征向量,如果
依次是与之对应的特征向量,如果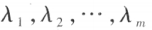 各不相等,则
各不相等,则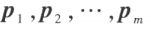 线性无关。
线性无关。
设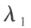 和
和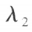 是方阵 **A **的两个不同特征值,
是方阵 **A **的两个不同特征值,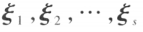 和
和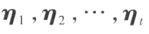 分别对应于
分别对应于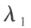 和
和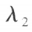 的线性无关的特征向量,则
的线性无关的特征向量,则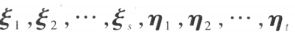 线性无关。
线性无关。
设 A、B 都是 n 阶矩阵,若有可逆矩阵P,使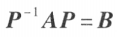 ,则称 B 是 A 的相似矩阵,或说矩阵 A 与 B 相似。
,则称 B 是 A 的相似矩阵,或说矩阵 A 与 B 相似。
若 n 阶矩阵 A 与 B 相似,则 A 与 B 的特征多项式相同,从而 A 与 B 的特征值亦相同。
若 n 阶矩阵 A 与对角矩阵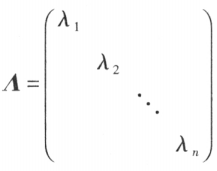 相似,则
相似,则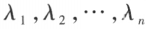 即是 A 的 n 个特征值。
即是 A 的 n 个特征值。
n 阶矩阵 **A **与对角矩阵相似(即 A 能对角化)的充分必要条件是 A 有 n 个线性无关的特征量。
如果 n 阶矩阵 A 的 n 个特征值互不相等,则 A 与对角矩阵相似。
对称矩阵的特征值为实数。
设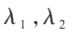 是对称矩阵A的两个特征值,
是对称矩阵A的两个特征值,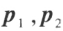 是对应的特征向量。若
是对应的特征向量。若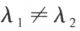 ,则
,则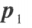 与
与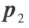 正交。
正交。
设 A 为 n 阶对称矩阵,则必有正交矩阵P,使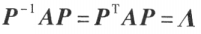 ,其中
,其中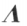 是以
是以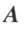 的 n 个特征值为对角元的对角矩阵。
的 n 个特征值为对角元的对角矩阵。
设 A 为 n 阶对称矩阵,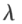 是 A 的特征方程的 k 重根,则矩阵
是 A 的特征方程的 k 重根,则矩阵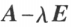 的秩
的秩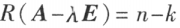 ,从而对应特征值
,从而对应特征值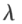 恰有 k 个线性无关的特征向量。
恰有 k 个线性无关的特征向量。
含有 n 个变量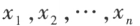 的二次齐次函数
的二次齐次函数
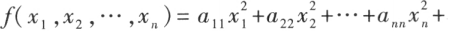
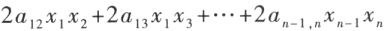 称为二次型。
称为二次型。
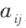 为复数时,
为复数时,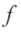 称为复二次型;当
称为复二次型;当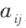 为实数时,
为实数时,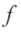 称为实二次型。
称为实二次型。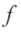 的矩阵,也把
的矩阵,也把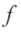 叫做对称矩阵 A 的二次型,对称矩阵A的秩就叫做二次型
叫做对称矩阵 A 的二次型,对称矩阵A的秩就叫做二次型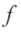 的秩。
的秩。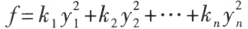
只含有平方项的二次型,称为二次型的标准形(或法式)。
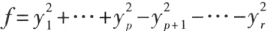
如果标准形的系数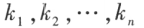 只在 1 , -1 , 0 三个数中取值,则称为二次型的规范形。
只在 1 , -1 , 0 三个数中取值,则称为二次型的规范形。
设 A 和 B 是 n 阶矩阵,若有可逆矩阵 C ,使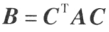 ,则称矩阵 A 与 B 合同。
,则称矩阵 A 与 B 合同。
任给二次型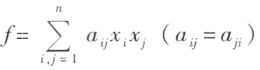 ,总有正交变换
,总有正交变换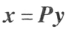 ,使
,使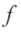 化为标准形
化为标准形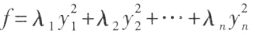 ,其中
,其中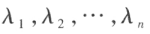 是
是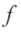 的矩阵
的矩阵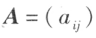 的特征值。
的特征值。
任给 n 元二次型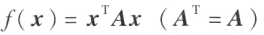 ,总有可逆变换
,总有可逆变换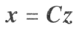 ,使
,使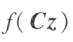 为规范形。
为规范形。
设二次型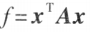 的秩为 r ,且有两个可逆变换
的秩为 r ,且有两个可逆变换 使
使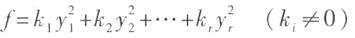 或
或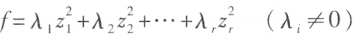 ,则
,则 中正数的个数与
中正数的个数与 中正数的个数相等。
中正数的个数相等。
设二次型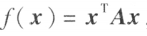 ,如果对任何
,如果对任何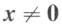 ,都有
,都有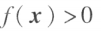 (显然
(显然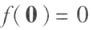
),则称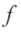 为正定二次型,并称对称矩阵 A 是正定的;如果对任何
为正定二次型,并称对称矩阵 A 是正定的;如果对任何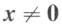 都有
都有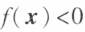 ,则称
,则称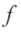 为负定二次型,并称对称矩阵 A 是负定的。
为负定二次型,并称对称矩阵 A 是负定的。
n 元二次型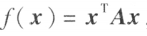 为正定的充分必要条件是:它的标准形的 n 个系数全为正,即它的规范形的 n 个系数全为 1 ,亦即它的正惯性指数等于 n 。
为正定的充分必要条件是:它的标准形的 n 个系数全为正,即它的规范形的 n 个系数全为 1 ,亦即它的正惯性指数等于 n 。
对称矩阵 A 为正定的充分必要条件是:A 的特征值全为正。
对称矩阵 A 为正定的充分必要条件是:A 的各阶主子式都为正,
即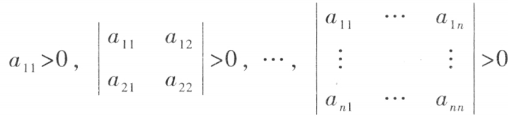 ,
,
对称矩阵A为负定的充分必要条件是:奇数阶主子式为负,而偶数阶主子式为正,
即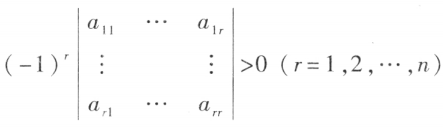
原文:https://www.cnblogs.com/xiaolistudent/p/15139841.html