博文地址

目录

13 | 线性排序：如何根据年龄给100万用户数据排序？

今天讲的是三种时间复杂度是 O(n) 的排序算法：桶排序、计数排序、基数排序。

因为这些排序算法的时间复杂度是线性的，所以我们把这类排序算法叫作线性排序（Linear sort）。

之所以能做到线性的时间复杂度，主要原因是，这三个算法是非基于比较的排序算法，都不涉及元素之间的比较操作。

这几种排序算法理解起来都不难，时间、空间复杂度分析起来也很简单，但是对要排序的数据要求很苛刻，我们学习的重点是掌握这些排序算法的适用场景。

总结

• 桶排序时间复杂度是O(n+k)，计数排序时间复杂度是O(n+k)，基数排序时间复杂度是O(n*k)
• 桶排序空间复杂度是O(n)，计数排序空间复杂度是O(k)，基数排序空间复杂度是O(n+k)
• 都是稳定的排序算法

桶排序 Bucket sort

核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

时间复杂度分析

• 如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。
• 每个桶内部使用快速排序，时间复杂度为 O(k * logk)。
• m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。
• 当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

桶排序对要排序数据的要求

• 首先，要排序的数据需要很容易就能划分成 m 个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。
• 其次，数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果数据都被划分到一个桶里，那就退化为 O(nlogn) 的排序算法了。

桶排序比较适合用在外部排序中

所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。

比如说我们有 10GB 的订单数据，我们希望按订单金额进行排序，但是我们的内存有限，只有几百 MB，这个时候该怎么办呢？

• 我们可以先扫描一遍文件，看订单金额所处的数据范围。假设经过扫描之后我们得到，订单金额最小是 1 元，最大是 10 万元。
• 我们将所有订单根据金额划分到 100 个桶里，第一个桶我们存储金额在 1 元到 1000 元之内的订单，第二桶存储金额在 1001 元到 2000 元之内的订单，以此类推。每一个桶对应一个文件，并且按照金额范围的大小顺序编号命名（00，01，02...99）。
• 理想的情况下，如果订单金额在 1 到 10 万之间均匀分布，那订单会被均匀划分到 100 个文件中，每个小文件中存储大约 100MB 的订单数据，我们就可以将这 100 个小文件依次放到内存中，用快排来排序。
• 等所有文件都排好序之后，我们只需要按照文件编号，从小到大依次读取每个小文件中的订单数据，并将其写入到一个文件中，那这个文件中存储的就是按照金额从小到大排序的订单数据了。

如果订单金额分布不均匀，可以对数据较多的区间再次使用桶排序划分为更小的区间。

计数排序 Counting sort

计数排序其实是桶排序的一种特殊情况。

当要排序的 n 个数据所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。

比如，高考考生成绩排名。

计数排序动图

这个动图并不准确，其更像是桶排序的过程，因为看起来他是先把待排的元素一个个的放到了桶里，这样的空间复杂度只能是O(n)，就没法优化为O(k)。

计数排序过程分析

假设有 8 个考生，其成绩放在一个数组 A[8] 中：2,5,3,0,2,3,0,3。考生的成绩从 0 到 5 分，我们使用大小为 6 的数组 C[6] 表示桶，其中下标为分数、值为对应的考生个数。

• 首先我们需要遍历一遍考生分数，然后就可以得到 C[6] 的值：[2,0,2,3,0,1]
• 从中可以看出，分数为 3 分的考生有 3 个，小于 3 分的考生有 4 个
• 所以，成绩为 3 分的考生在排序之后的有序数组 R[8] 中，会保存在下标为 4，5，6 的位置

那我们如何快速计算出每个分数的考生在有序数组中对应的存储位置呢？

• 我们首先对 C[6] 数组顺序求和，求和后 C[k] 里存储的就是小于等于分数 k 的考生个数。顺序求和后 C[6] = [2,2,4,7,7,8]

• 我们从后到前依次扫描数组 A：2,5,3,0,2,3,0,3
  • 比如，当扫描到 3 时，我们可以从数组 C 中取出下标为 3 的值 7，也就是说，到目前为止，包括自己在内，分数小于等于 3 的考生有 7 个，也就是说 3 是数组 R 中的第 7 个元素（也就是数组 R 中下标为 6 的位置）。当 3 放入到数组 R 中后，小于等于 3 的元素就只剩下了 6 个了，所以相应的 C[3] 要减 1，变成 6。
  • 以此类推，当我们扫描到第 2 个分数为 3 的考生的时候，就会把它放入数组 R 中的第 6 个元素的位置（也就是下标为 5 的位置）。
  • 当我们扫描完整个数组 A 后，数组 R 内的数据就是按照分数从小到大有序排列的了。

从数组 A 中取数，也是可以从头开始取，但是就不是稳定排序算法了(因为最先取到的元素会被放到后面)

总结

• 数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。
• 而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。

桶排序空间复杂度是O(n)，而计数排序空间复杂度是O(k)

基数排序 Radix sort

假设我们有 10 万个手机号码，希望将这 10 万个手机号码从小到大排序，你有什么比较快速的排序方法呢？

这个问题里有这样的规律：假设要比较两个手机号码 a，b 的大小，如果在前面几位中，a 手机号码已经比 b 手机号码大了，那后面的几位就不用看了。

排序过程

先按照最后一位来排序手机号码，然后再按照倒数第二位重新排序，以此类推，最后按照第一位重新排序。经过 11 次排序之后，手机号码就都有序了。

注意，这里按照每位来排序的排序算法一定要是稳定的。

时间复杂度分析

• 根据每一位来排序，我们可以用刚讲过的桶排序或者计数排序，它们的时间复杂度可以做到 O(n)
• 如果要排序的数据有 k 位，那我们就需要 k 次桶排序或者计数排序，总的时间复杂度是 O(k*n)
• 当 k 不大的时候，比如手机号码排序的例子，k 最大就是 11，所以基数排序的时间复杂度就近似于 O(n)

基数排序对要排序数据的要求

• 需要可以分割出独立的位来比较
• 位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了
• 每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了

实际上，有时候要排序的数据并不都是等长的，比如排序牛津字典中的 20 万个英文单词。这时，我们可以把所有的单词补齐到相同长度(比如在后面补0)，这样就可以继续用基数排序了。

14 | 排序优化：如何实现一个通用的、高性能的排序函数？

如何选择合适的排序算法？

• 线性排序算法的时间复杂度虽然比较低，但适用场景比较特殊，所以不适合作为通用的排序函数。
• 如果对小规模数据进行排序，可以选择时间复杂度是 O(n^2) 的算法
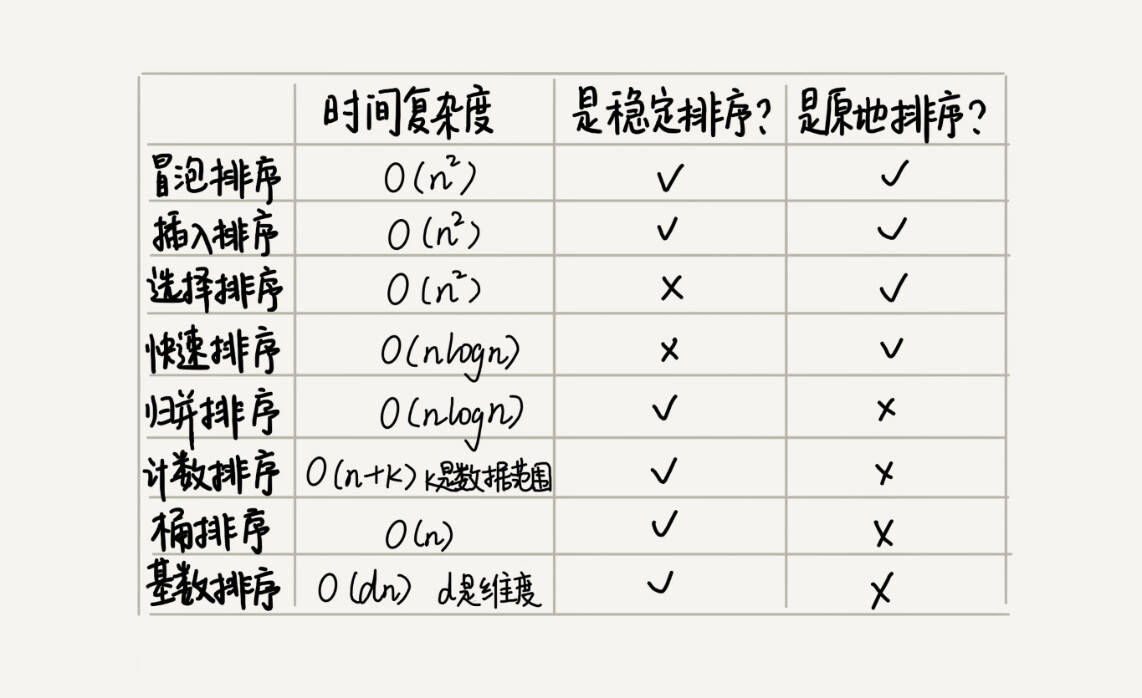
• 如果对大规模数据进行排序，时间复杂度是 O(nlogn) 的算法更加高效

为了兼顾任意规模数据的排序，一般都会首选时间复杂度是 O(nlogn) 的排序算法来实现排序函数。

• 归并排序可以做到平均情况、最坏情况下的时间复杂度都是 O(nlogn)，但是归并排序不是原地排序算法，空间复杂度是 O(n)，占用空间过大
• 快速排序空间复杂度是O(logn)，虽然快速排序在最坏情况下的时间复杂度是 O(n^2)，但是有很多方法可以优化

如何优化快速排序？

时间复杂度退化为O(n^2)的主要原因是因为我们分区点选得不够合理。

为了提高快速排序算法的性能，我们要尽可能地让每次分区都比较平均。最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。

两个比较常用、比较简单的分区算法：

• 三数取中法：从区间的首、尾、中间，分别取出一个数，然后取这 3 个数的中间值作为分区点
• 随机法：每次从要排序的区间中，随机选择一个元素作为分区点

分析 C 语言中的排序函数 qsort()

虽说 qsort() 从名字上看，很像是基于快速排序算法实现的，实际上它并不仅仅用了快排这一种算法。

• 要排序的数据量比较小的时候，qsort() 会优先使用归并排序
  • 对于小数据量的排序，归并排序需要额外内存空间的问题不大，用空间换时间
• 要排序的数据量比较大的时候，qsort() 会改为用快速排序
  • qsort() 选择分区点的方法就是三数取中法
  • qsort() 通过自己实现一个堆上的栈，手动模拟递归来解决递归太深会导致堆栈溢出的问题
• 在快速排序的过程中，当要排序的区间中元素的个数小于等于 4 时，qsort() 就退化为比较简单、不需要递归的插入排序
  • 因为在小规模数据面前，O(n^2) 时间复杂度的算法并不一定比 O(nlogn) 的算法执行时间长
  • 在 qsort() 插入排序的算法实现中，也利用了哨兵这种编程技巧。虽然哨兵可能只是少做一次判断，但是毕竟排序函数是非常常用、非常基础的函数，性能的优化要做到极致。

2021-8-13

数据结构与算法之美-5 排序算法3 [MD]

原文：https://www.cnblogs.com/baiqiantao/p/15139455.html