写了前面几篇文章,其实面对大部分的场景来说应该是够用了,但是在PID中还有一个自适应版本的PID让我觉得十分神奇,所以打算把这个算法也填一填坑。
如今神经网络研究的火爆也让许多的控制领域学者开始将神经网络与自动控制相结合起来,其中的原因主要是神经网络的几大特性:
单神经元自适应PID控制器就是使用单神经元控制的,可以实现自行调整系统PID参数的PID控制器。
其实自适应的PID还有其他的控制方式,本篇文章就只是介绍以单神经元控制的自适应PID控制器。(下文简称自适应PID控制器)
自适应PID与普通的PID算法最大的区别就是它能够根据系统的性质的改变从而自行调整PID的参数,而普通的PID算法则无法做到这一点。
在工业控制上,有很多的PID系统的运行时间极长,与我们平时做的平衡小车等玩意不同,工业设施在长时间的运转过程中其自身的物理性质是很容易发生改变的,比如更换了不同的零件、设施本身发生了腐蚀等等。一旦物理性质发生了改变,那么原来出厂时设定的PID参数就不是当前系统的最佳设定了。而如果设施采用的自适应的PID算法,它就能在运行的过程中不断修正自己的PID参数设定,从而保证系统一直都工作在最佳的状态。
综合看来,自适应PID的强大之处在于其的自适应能力,后面会详细介绍它是如何实现的。首先我们先从神经元开始讲起。
脑袋中的神经元
神经元的大致结构就像下面这样:
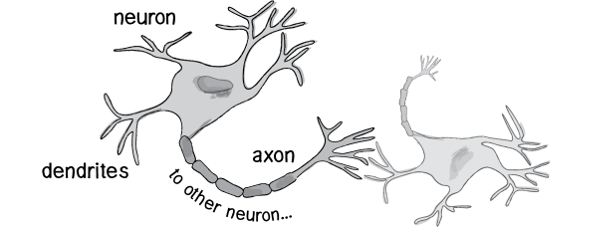
复习一下高初中的生物知识,神经元由细胞体与突起组成,而突起分为树突与轴突,树突就是上图中左侧的像网络一样的突起,它是一个接收器,与其他神经元细胞的轴突相连接,接受其他神经元细胞发出的信号;轴突就是上图中右侧的长条状的突起,是一个发射器,负责将信号发送给其他的神经元细胞。
无数的神经元组成了一个庞大的神经网络,叫做神经中枢,而人能够产生各种行为,就是根据神经中枢传出的指令而做出的反应。
芯片中的神经元
文章中所说的并不是生物大脑中的神经元,而是科学家们通过了解生物神经元的结构之后使用计算机模拟出来的一种计算机结构。为什么科学家会模拟大脑?原因是希望能将大脑“思考”的能力赋予给机器。
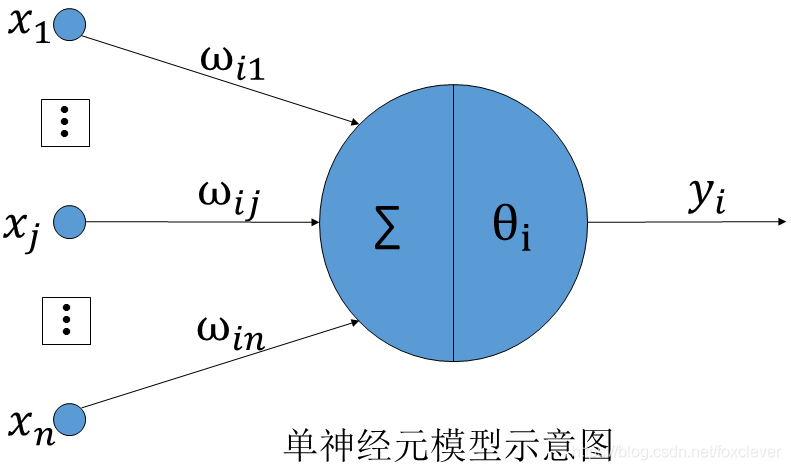
最简单的神经元模型叫做“感知器”,长下面这个样子:

前面\(x_{1}\)、\(x_{2}\)、\(x_{3}\)模拟的就是生物神经元的树突,而\(output\)表示的就是神经元的轴突。无数个这样的神经元前后连接,就形成了芯片中的“大脑”。
但是常用的神经元模型的树突上还会加上“权重”,输入与权重相乘后相加,如果最后的值大于神经元的阈值,神经元就会产生一个\(output\)信号,这就是模拟了生物大脑中只有当一个神经元受到足够大的刺激才能产生电信号的过程。
有:
其中神经元的阈值项\(\theta_{i}\)表示,只有输入的值的线性和大于这个值,神经元才会有输出。
学习规则
学习规则可以使得模拟出来的神经元通过某种方式得到“学习”的能力。它主要的功能是实现对神经元之间的连接强度的修正,即修改“权重”。不同的学习规则可以形成不同的神经网络,这些神经网路的具体性质也有不同。较为常用的学习规则有Hebb、Perceptron、Delta、BP等。
学习分为无监督学习和监督学习,简单区分就是是否引入了期望值。通用的学习规则如下:
表达式表示的意思是权重在t时刻的差值\(\Delta W_{j(t)}\)与t时刻的输入\(x(t)\)和学习信号\(r\)的乘积成正比,这里的比例系数是\(\eta\),也称为学习常数,决定了学习的速率。
所以可以得到下一时刻的加权:
这里采用的神经元学习规则为有监督Hebb学习规则,可选用的规则并不局限于此。有监督的Hebb学习规则是Hebb学习规则与\(\Delta\)学习规则的结合,所以下面介绍一下学习规则的相关信息。
Hebb学习规则默认所说的就是无监督的Hebb规则,后面人们提出了有监督的Hebb规则以适应不同模型的需要。Hebb学习规则其实与“条件反射”的机理一致。
相信大家都还记得生物书上巴普洛夫做过一个著名的实验以研究条件反射:
Hebb理论认为同一时间被激活的两个神经元(网络)之间的联系会被强化,从而让细胞记忆这两个事物之间存在着联系。相反如果这两个事物的联系越来越弱,那么这两个神经元(网络)之间的联系也就越来越被弱化。
Hebb学习规则就是通过调整神经元联结的权重来起到了“学习”的作用,也就是:权值的差值与输入输出的乘积呈正比例关系。
运用上边的公式\((2)\),可以看出如果一个树突结构(一个输入)经常有输入产生,那么在这条路线上的权值就会随着时间不断地累积,正好对应了上面所说的“同一时间被激活的两个神经元(网络)之间的联系会被强化”。但是最开始的Hebb学习并没有“弱化”的过程。
无监督的Hebb学习规则的学习表达式如下:
其中\(\Delta w_{j}(t)\)、\(\eta\)、\(X_{i}(t)\)、\(Y_{j}(t)\)分别表示权值的差值、学习速率、上一个神经元对此神经元的输入(即理解为当前神经元的输入)、当前神经元对下一个神经元的输入(即理解为当前神经元的输出)。
首先作为一个有监督的学习规则,所以学习的过程中就必须引入期望值了。这里设期望值为\(y\),而当前神经元输出的值为\(\hat{y}\)。现在我们就能得到二者的差值了,不过在这里一般使用类似方差的方式来描述:
其中\(E\)就是所求的误差(是不是感觉跟前面PID控制器中的差值都是类似的东西?)
不管差值的形式如何,为了让学习的效果最大化,肯定是要让这个差值越小越好。它是一个\(y\)关于\(E\)的二次函数,但是我们需要讨论的是误差值\(E\)与权值的差值\(\Delta w_{ij}\)的关系。它们之间肯定也是呈一个凹函数的关系,那么我们只要找到它的最低点就好了,不是吗?
但是事情没有这么简单。神经元的学习差值函数并不是一个值都是已知的函数,我们只知道过去的以及当前的\(E\),对还未通过神经元的输入无法知道其输出值,这就无法直接计算了。所以我们采用的是梯度下降法:神经元通过一次次的迭代,每一次都根据当前输出的值做一次修正,直到找到目标误差函数的最小值。这就类似于我们如果想要找到一个山谷的最低处,我们只要一直往比当前低的地方走,直到没有更低的地方就好了。当然这其中可能会有比当前最低处更低的地方没有被发现,误以为当前的深度就是最低点的情况。只是对于本文讨论的单个神经元模型来说,并没有这种复杂的情况。
为了求得\(E\)上的最低点,我们对\((4)\)求\(E\)关于权值的偏导,有:
其中\(g\)表示的是激活函数,这个函数模拟的就是神经元的输出值,恒为正数。但简单来看,也可把中间这一步骤略去,因为非负值对权值的修正方向没有影响。所以\((5)\)式化简得到:
现在我们就得到了修正的规则,\(\Delta\)规则:权值的差值与当前输出值与期望之差和输入的乘积呈正比关系。
其学习规则的表达式为:
随着\(\Delta\)学习规则的不断调用,神经元会不断修正自己每一个树突上的权值,从而使得输出值向给出的期望值靠近。(听上去是不是有PID那味儿了?还没完呢!)这个修正的过程对于单神经元来说,权值的差值是一个负值。
等等,负值!前面的Hebb学习规则不就是没有“弱化”的过程吗?
为了解决hebb学习规则没有“弱化”连接神经元的过程,所以我们用有监督的\(\Delta\)学习规则与其相乘,便得到了有监督的Hebb学习规则,这个学习规则可以在给定期望值的情况下将同一时间被激活的两个神经元(网络)之间的联系强化,从而让神经元记忆这两个事物之间存在着联系;相反如果这两个事物的联系越来越弱,那么这两个神经元之间的联系也就越来越被弱化。
其学习规则的表达式为:
学了那么久的计算机科学,你是否又开始想念我们的控制理论了呢?下面我们就将先前的PID控制论移植到神经元中去。
在这里我们还是选择将算法移植到增量式的PID算法中。(位置式PID:呜呜呜)
还是将增量式的PID表达式搬出来:
在这里可以将PID本身看作一个单神经元:三个树突分别是以上式子中的三项差值,输出就是轴突,其中三个PID参数就是三个树突的权值。为了对应单神经元的学习速率,我们再引入一个比例系数\(K\)好了。
所以上面这个增量式的PID表达式就被我们改写成了下面这个样子:
其中\({W}‘\)PID的参数,也就是神经元树突的权值,计算的方式为:
我们将PID的输出直接写出来,并将PID参数的调整用前面的学习规则来书写,有:
式中:
可以看到在计算PID的三个参数的时候,其参数的权值增量使用了前面推导出来的有监督的Hebb学习规则来调整:学习速率直接照搬,误差值也就是PID中的误差值\(err(t)\);系统的输入便是上面的三个式子;系统的输出便是\(u(t)=u(t-1)+\Delta u(t)\).
其中(t-1)代表的就是上一时刻的量;我们在PID中需要的三个PID参数\(K_{p}\)、\(K_{I}\)、\(K_{D}\)分别对应着上面的\(w_{1}(t)\)、\(w_{2}(t)\)、\(w_{3}(t)\);\(\eta _{p}\)、\(\eta _{I}\)、\(\eta _{D}\)分别是比例、积分、微分项的学习速率,采用不同的学习速率的原因是以便对不同的权重进行分别调整。
这里还有最后一个参数的值需要确定:那就是我们引入的\(K\).K值的选择十分重要,可以看到K值越大则PID调整的也就越快速,但是如果过快的话会使得系统运行不稳定(类似单P控制)。所以一般来说当被控制的对象时延增大的时候K值必须减小以保证系统的稳定,但是K值如果设置得过小,又会使得系统得快速稳定性变差。
至此单神经元自适应PID控制器就已经被完全推导出来了。
在大量的实际运用中,人们发现PID的在线学习修正主要与\(e(t)\)与\(\Delta e(t)\)有关,所以人们索性将PID三个参数的学习公式都改成了下面的形式:
其中\(\Delta e(t)=e(t)-e(t-1)\)。改进之后权重的在线修正就不再完全是根据神经网络的学习原理而是参杂了实际经验的考虑了。
有了前面的算法基础,我们就可以开始将他们转换成代码实现了。这里没有使用改进的算法,而还是使用原本的纯神经元自适应PID算法。
首先还是定义一个结构体,在其中准备算法所需要的变量:
/*定义结构体和公用体*/
typedef struct
{
float setpoint; /*设定值*/
float kcoef; /*神经元输出比例*/
float kp; /*比例学习速度*/
float ki; /*积分学习速度*/
float kd; /*微分学习速度*/
float lasterror; /*前一拍偏差*/
float preerror; /*前两拍偏差*/
float deadband; /*死区*/
float result; /*输出值*/
float output; /*百分比输出值*/
float maximum; /*输出值的上限*/
float minimum; /*输出值的下限*/
float wp; /*比例加权系数*/
float wi; /*积分加权系数*/
float wd; /*微分加权系数*/
}NEURALPID;
这一步是先先给PID参数赋一个基础值,目的是让PID的自适应功能先运转起来,后面这些值都会改变的。
/* 单神经元PID初始化操作,需在对vPID对象的值进行修改前完成 */
/* NEURALPID vPID,单神经元PID对象变量,实现数据交换与保存 */
/* float vMax,float vMin,过程变量的最大最小值(量程范围) */
void NeuralPIDInitialization(NEURALPID *vPID,float vMax,float vMin)
{
vPID->setpoint=vMin; /*设定值*/
vPID->kcoef=0.12; /*神经元输出比例*/
vPID->kp=0.4; /*比例学习速度*/
vPID->ki=0.35; /*积分学习速度*/
vPID->kd=0.4; /*微分学习速度*/
vPID->lasterror=0.0; /*前一拍偏差*/
vPID->preerror=0.0; /*前两拍偏差*/
vPID->result=vMin; /*PID控制器结果*/
vPID->output=0.0; /*输出值,百分比*/
vPID->maximum=vMax; /*输出值上限*/
vPID->minimum=vMin; /*输出值下限*/
vPID->deadband=(vMax-vMin)*0.0005; /*死区*/
vPID->wp=0.10; /*比例加权系数*/
vPID->wi=0.10; /*积分加权系数*/
vPID->wd=0.10; /*微分加权系数*/
}
下面是增量式单神经元自适应PID控制器的算法部分:
/* 神经网络参数自整定PID控制器,以增量型方式实现 */
/* NEURALPID vPID,神经网络PID对象变量,实现数据交换与保存 */
/* float pv,过程测量值,对象响应的测量数据,用于控制反馈 */
void NeuralPID(NEURALPID *vPID,float pv)
{
float x[3];
float w[3];
float sabs
float error;
float result;
float deltaResult;
error=vPID->setpoint-pv;
result=vPID->result;
if(fabs(error)>vPID->deadband)
{
x[0]=error;
x[1]=error-vPID->lasterror;
x[2]=error-vPID->lasterror*2+vPID->preerror;
sabs=fabs(vPID->wi)+fabs(vPID->wp)+fabs(vPID->wd);
w[0]=vPID->wi/sabs;
w[1]=vPID->wp/sabs;
w[2]=vPID->wd/sabs;
deltaResult=(w[0]*x[0]+w[1]*x[1]+w[2]*x[2])*vPID->kcoef;
}
else
{
deltaResult=0;
}
result=result+deltaResult;
if(result>vPID->maximum)
{
result=vPID->maximum;
}
if(result<vPID->minimum)
{
result=vPID->minimum;
}
vPID->result=result;
vPID->output=(vPID->result-vPID->minimum)*100/(vPID->maximum-vPID->minimum);
//单神经元学习
NeureLearningRules(vPID,error,result,x);
vPID->preerror=vPID->lasterror;
vPID->lasterror=error;
}
这里是有监督的Hebb学习规则的算法部分:
/*单神经元学习规则函数*/
static void NeureLearningRules(NEURALPID *vPID,float zk,float uk,float *xi)
{
vPID->wi=vPID->wi+vPID->ki*zk*uk*xi[0];
vPID->wp=vPID->wp+vPID->kp*zk*uk*xi[1];
vPID->wd=vPID->wd+vPID->kd*zk*uk*xi[2];
}
在推导公式之前我曾经试过硬啃代码,结果发现啃了个寂寞……但是在一顿推导猛如虎之后,发现代码实现其实是一件很简单的事情。(我记得这事好像教我数据结构的老师说过……老师我学废了)
在这一段时间的PID算法学习过程中,逐渐发现了算法以及仿真验证的重要性。自己先前主力学习的是硬件设计等,以为会设计几块电路,能驱动单片机就学到头了,结果发现外面的世界是多么地广大。
上面的代码是一位老哥在对照着Matlab的仿真代码移植到C中的。谈到MatLab,我也不禁感叹这个巨无霸工业软件能力的恐怖如斯。美帝对华部分的封锁中也包含着对matlab的禁用,这对许多科学研究来说都是一场不小的灾难。希望我们能够卧薪尝胆,早日摆脱帝国主义的技术封锁,实现中华的技术无限突破。
[1]佚名. 单神经元自适应PID控制器设计. 辽宁科技大学本科生毕业设计论文
[2]郝志红. 单神经元自适应PID控制算法. 《冶金自动化》2012S1
[3]单神经元PID控制器的实现:https://blog.csdn.net/foxclever/article/details/84678393
[4]人工神经元和Delta规则:https://zhuanlan.zhihu.com/p/23478187
[5]深度学习 --- 神经网络的学习原理(学习规则):https://blog.csdn.net/weixin_42398658/article/details/83816633
[6]《先进PID控制MATLAB仿真》第四版 刘金琨编著
原文:https://www.cnblogs.com/ren-jiong/p/15124089.html