408算法练习——最大正方形（动态规划）

最大正方形

题目链接：https://leetcode-cn.com/problems/maximal-square/

一、问题描述

　　在一个由 ‘0‘ 和 ‘1‘ 组成的二维矩阵内，找到只包含 ‘1‘ 的最大正方形，并返回其面积。

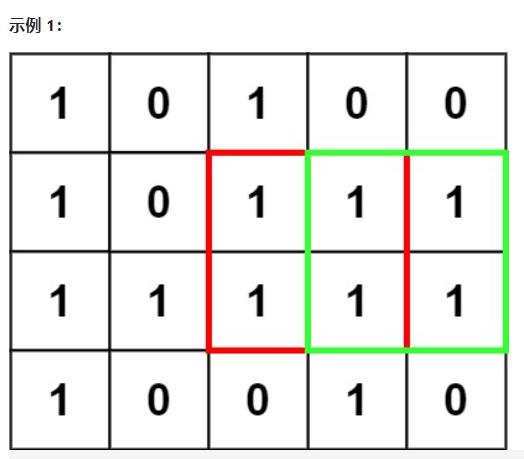
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

二、问题分析

　　题目要求找出矩阵中的最大正方形，为了避免重复遍历相同元素应该使用动态规划算法，分析以下几个问题

　　动态规划的数组该如何定义数组元素的含义？

　　该如何定义状态转移方程？

　　最后的结果怎么得出？

　　动态规划数组形式：如果用数组元素表示从(0,0)到（i，j）这个图形中的最大正方形的边长可以吗？可以列一个例子试一下，显然是难以实现，因为状态转移方程很难定义，分析原因不难发现，其实在整个矩阵中散落着无数个正方形，这些正方形可能是相互间隔开的，这样在使用状态转移方程时难以确定动规数组元素的值。因为无法把这个数组中的最大值累计到后面的数组中。原因就是0的干扰使得数组元素值无法向后继续传递。这部分需要一定的理解。那么该如何定义数组元素的值？如果我们把每个小正方形看作一个整体，那么（i，j）的含义就是以该元素为右下角能构造出的正方形的最大边长。

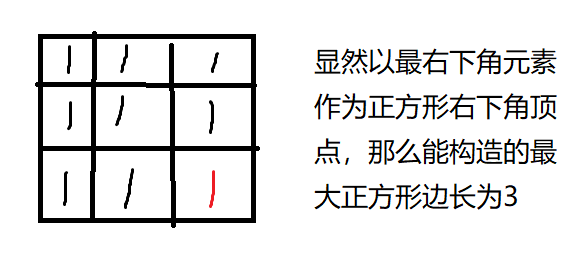
　　如图，如果动规数组中每个元素都表示以矩阵中该位置元素为右下角顶点可构成的的最大正方形边长，那么在最后只需要找出动规数组中的最大值就能得出结果。

　　如何定义状态转移方程呢？假设当前元素是0，那么显然以该元素为右下角就无法构成正方形，所有动规数组应该填0；如果当前元素为1，就必须结合该元素左侧，上侧，左上方的元素综合判断，如果把这个1加入以上三个元素构成的正方形中能否构成更大的正方形？条件是以上三个元素的值必须相同。如果对这个判断再做推广

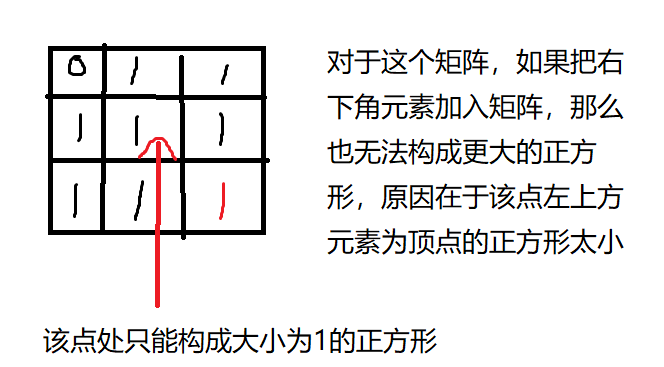
 　　所有只能取左侧，上侧，左上侧元素中的最小值进行计算，可以反证这个结论，如果取最大值进行计算，那么就会忽略掉某些位置而无法构成正方形。

　　对于最终结果，只需要遍历动规数组取出最大值即可，可以在规划过程中记录最大值。

 三、代码

 1 class Solution {
 2     public int maximalSquare(char[][] matrix) {
 3 
 4         int rows = matrix.length, columns = matrix[0].length;
 5         int[][] dp = new int[rows][columns];
 6         int maxlen = 0;
 7         for(int i=0;i<rows;i++){
 8             for(int j=0;j<columns;j++){
 9                 if(matrix[i][j] == ‘1‘){
10                     if(i==0||j==0){
11                         dp[i][j]=1;
12                     }else{
13                          dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
14                     }   
15                 }else{
16                    dp[i][j]=0;
17                 }
18                 maxlen = Math.max(maxlen,dp[i][j]);
19             }
20         }
21         return maxlen*maxlen;
22     }
23 }

408算法练习——最大正方形（动态规划）

原文：https://www.cnblogs.com/zyq79434/p/15091816.html