① diag(A):提取矩阵A主对角线元素,产生一个列向量;
② diag(A,k):提取矩阵A第k条对角线的元素,产生一个列向量;
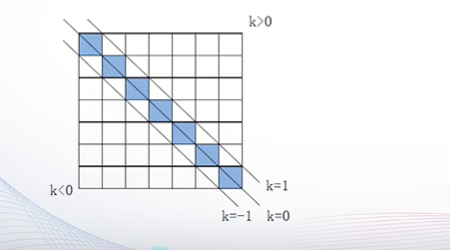
① diag(V):以向量 V 为主对角线元素,产生对角矩阵。
② diag(V,k):以向量 V 为第 k 条对角线元素,产生对角矩阵。
>> A=[7,0,1,0,5;3,5,7,4,1;4,0,3,0,2;1,1,9,2,3;1,8,5,2,9]
A =
7 0 1 0 5
3 5 7 4 1
4 0 3 0 2
1 1 9 2 3
1 8 5 2 9
>> D = diag(1 : 5)
D =
1 0 0 0 0
0 2 0 0 0
0 0 3 0 0
0 0 0 4 0
0 0 0 0 5
>> D * A
ans =
7 0 1 0 5
6 10 14 8 2
12 0 9 0 6
4 4 36 8 12
5 40 25 10 45
① triu(A) :提取矩阵A的对角线及以上的元素。
② triu(A,k) : 提取矩阵A第k条对角线及以上的元素。
ones(4)//生成四阶全为一的矩阵
>> triu(ones(4),-1)
ans =
1 1 1 1
1 1 1 1
0 1 1 1
0 0 1 1
tril 是提取矩阵A的下三角矩阵的函数,用法与triu函数相同。
rot90(A,k): 将矩阵A逆时针方向旋转90的 k 倍,当k = 1时可省略;
>> A=[1,3,2;-3,2,1;4,1,2]
A =
1 3 2
-3 2 1
4 1 2
>> rot90(A)// 逆时针90
ans =
2 1 2
3 2 1
1 -3 4
>> rot90(A,2)//逆时针180
ans =
2 1 4
1 2 -3
2 3 1
①fliplr(A): 对矩阵A实施左右翻转。
②flipud(A): 对矩阵A实施上下翻转。
inv(A): 求方阵A的逆矩阵。

>> A = [1,2,3;1,4,9;1,8,27];
>> b = [5;-2;6];
>> x = inv(A) * b
x =
23.0000
-14.5000
3.6667
>> x = A\b
x =
23.0000
-14.5000
3.6667
原文:https://www.cnblogs.com/rongrongrong/p/15034264.html