Let $r_1$ and $r_2$ be the radius of two concenter circles with $r_1<r_2$.
Point $A$ is moving at constant speed on the circle with radius $r_2$, and point $B$ is moving at constant speed on the circle with radius $r_1$.
The midpoint of line $AB$ makes some interesting diagrams.
For example, if $r_2=2r_1$, the resulting shape is a cardioid.
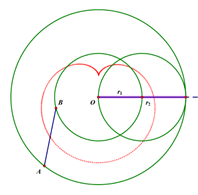
If $r_2=3r_1$, there is something like Garfield’s eyes.
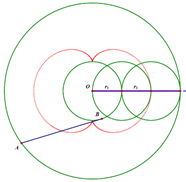

For $r_2=4r_1$, the shape is reminiscent of a nice clover.
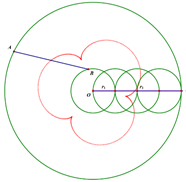
When $r_2=6r_1$, there is a blooming Catharanthus roseus.
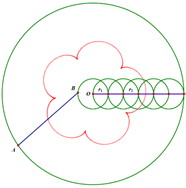
In general, for $r_2=kr_1$, the “flower” has $(k-1)$ “petals”.
原文:https://www.cnblogs.com/hazel-wu/p/15029637.html