最长公共子序列
一、问题描述
给定两个字符串或数字序列A和B,求一个字符串,使得这个字符串是A和B的最长公共部分(子序列可以不连续),返回长度
案例,字符串"sadstory"和"adminsorry"的最长公共子序列为"adsory"
二、问题分析
暴力解法,假设A和B的长度为n和m,那么找出A在所有子序列时间复杂度为2^n,找出B的所有子序列时间复杂度为2^m,然后依次比较所有子序列需要的时间复杂度为m+n,所以总的时间复杂度2^n+m。显然这个算法是不可接受的。
接下来构思动态规划算法:定义两个指针,分别指向A和B,两个指针依次向后遍历,并记录此时A[1,i],B[1,j]两个序列的最长公共子序列的长度。将这个长度存入dp[i][j]。
遍历过程,先固定i,然后j遍历一次,更新dp[i][j]中对应内容,然后i移动一位再次遍历j,总共有m*n次遍历。
遍历时,如果A[I]=A[j]那么dp[i][j]=dp[i-1][j-1]。
如果不相等那么dp[i][j]=max(dp[i-1][j],dp[i][j-1])
三、代码
1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 using namespace std; 5 const int N = 100; 6 char A[N],B[N]; 7 int dp[N][N]; 8 int main(){ 9 int n; 10 gets(A+1); 11 gets(B+1); 12 int lenA = strlen(A+1); 13 int lenB = strlen(B+1); 14 for(int i=0;i<=lenA;i++){ 15 dp[i][0] = 0; 16 } 17 for(int j=0;j<=lenB;j++){ 18 dp[0][j] = 0; 19 } 20 for(int i=i;i<=lenA;i++){ 21 for(int j=1;j<=lenB;j++){ 22 if(A[i]==B[j]){ 23 dp[i][j]=dp[i-1][j-1]+1; 24 }else{ 25 dp[i][j]=max(dp[i-1][j],dp[i][j-1]); 26 } 27 } 28 } 29 printf("%d\n",dp[lenA][lenB]); 30 return 0; 31 }
四、分析
代码中关于动态规划数组dp的更新,可以想象一张二维表,假设行为i,列为j,这里就是指A和B的下标。那么第i行就记录了A串以i为终点的子串,和B串所有字串的最长子序和。对二维表的更新过程如图所示。
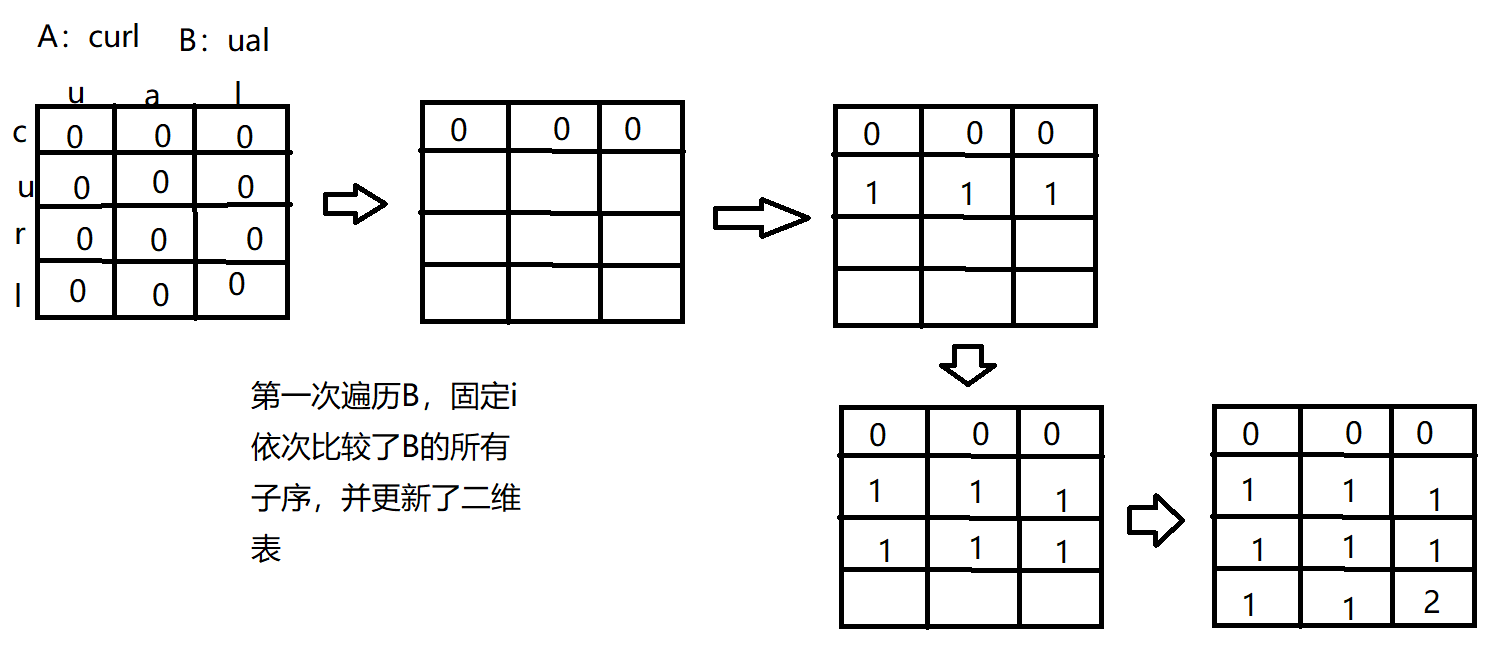
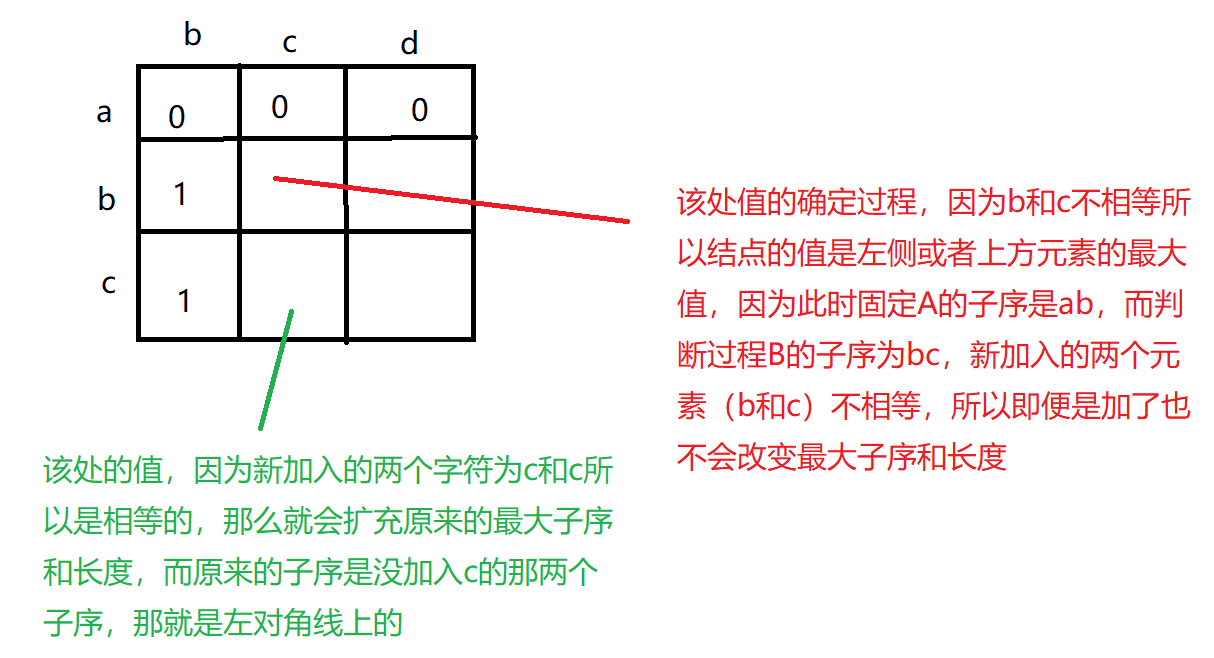
可以去看看最小生成树的弗洛伊德算法,和这个算法有异曲同工之处,其实对于A和B两个字符串其实就可以拆开成两个图,然后找两个图中的相同的有向路径,这么理解更为抽象,不过有利于理解算法。
原文:https://www.cnblogs.com/zyq79434/p/14924507.html