对本命专业测试算法与结果分布的简要分析

时间：2021-06-21 15:42:17 阅读：15 评论：0 收藏：0 [点我收藏+]

对本命专业测试算法与结果分布的简要分析

五月底发现并种草，事情实在有点多于是咕到现在

测试过程
- PC浏览器打开
  - 这个高级的自适应上来就给了我一个下马威，不得不说图片清晰度还不错
- Network分析
  - 点击F12后刷新，通过Network进行分析，可以看到收到大量png图片
  - 简单浏览一下，可以发现其中包含了全部题目和选项，但没有结果
  - 输入任意字符串开始答题，此时会发现收到另一批png图片，其中包含了全部可能的结果，共存在28种，~~看来这个测试的作者是个爽快人~~
- 寻找JavaScript
  - 既然题目和结果已经在测试开始前发送到本地，很自然的猜测计算结果也在本地完成，为此需要在JavaScript中寻找，一个可能的突破口是从按钮的点击事件入手分析，不过由于Network中只发现了三个JavaScript，依次浏览即可发现如下结构，进一步阅读此JavaScript中的代码可以得到从选项计算结果的算法
  - 此外，浏览这个JavaScript还可以发现，题目切换也在此实现，截取的部分代码如下，不过这并非本文重点，在此不做过多的讨论
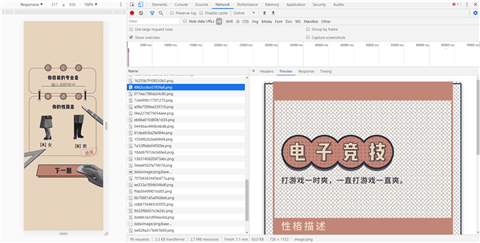
```
T = (t(123), [{
	key: "a",
	value: "文科"
}, {
	key: "b",
	value: "理科"
}, {
	key: "c",
	value: "再让我想想..."
}]),
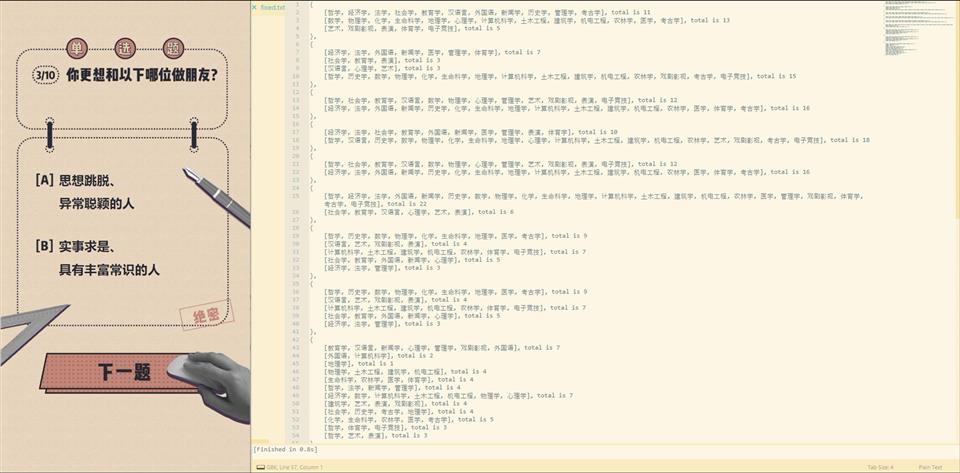
K = (t(124), [{
	key: "a",
	value: "外向且理性的人"
}, {
	key: "b",
	value: "外向但感性的人"
}, {
	key: "c",
	value: "内向且感性的人"
}, {
	key: "d",
	value: "内向但理性的人"
}]),
```
算法解析
- 算法完整代码如下
```
var J = function(A) {
	Array.prototype.shuffle || (Array.prototype.shuffle = function() {
		for (var A, e, t = this.length; t; A = parseInt(Math.random() * t),
			e = this[--t],
			this[t] = this[A],
			this[A] = e)
			return this
	});
	for (var e = {/* 见下表1 */}, t = [], n = 0; n < A.length; n++)
		for (var r = 0; r < A[n].length; r++) {
			var o = A[n][r], i = e[n][o];
			t = t.concat(i)
		}
	var a = {}, s = -1;
	t.shuffle();
	for (var l = 0; l < t.length; l++)
		void 0 === a[t[l]] && (a[t[l]] = 0),
		a[t[l]]++, -1 == s ? s = t[l] : a[t[l]] > a[s] && (s = t[l]);
	return s
},
```
- 算法流程描述如下
  - 第一阶段
    - 预先为每一题的的每个选项打若干专业标签(使用下面给出的表1)，合并前九题对应选项的标签列表为一个列表
      - 算法开始时，最终列表被初始化成一个空列表
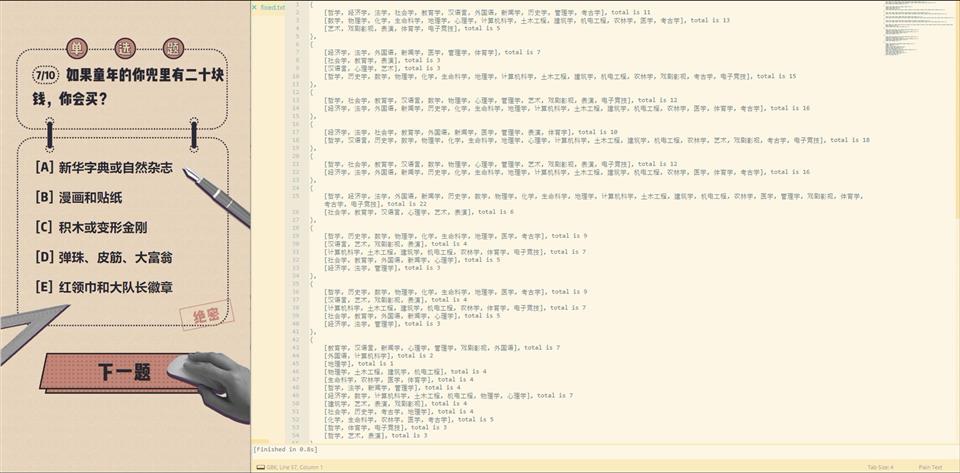
      - 以第一题选择C为例，第一题C选项的标签列表是[22, 23, 24, 25, 27]，选择了第一题C选项，那么最终列表会和[22, 23, 24, 25, 27]合并，即变为[22, 23, 24, 25, 27]
      - 以第二题选择C为例，第二题C选项的标签列表是[5, 14, 22]，选择了第二题C选项，那么最终列表会和[5, 14, 22]合并，即变为[22, 23, 24, 25, 27, 5, 14, 22]
      - 对其余题目以此类推，需要注意的是第九题是多选题，最终列表需要和每个选项对应的标签列表合并
    - 这一段的代码如下
```
for (var e = {/* 见下表1 */}, t = [], n = 0; n < A.length; n++)
	for (var r = 0; r < A[n].length; r++) {
		var o = A[n][r], i = e[n][o];
		t = t.concat(i)
	}
```
    - 其中A是选项id列表，t是最终列表，e[n][o]是第n题第o个选项的标签列表
    - 因为允许多选，选项id列表A中的每一项还是一个列表
    - 第一至八题是单选题，因此A中的第一至八项的列表中有且仅有一项，即满足A[n].length为1
    - 第九题是允许选2-3项的多选题，因此A中的这一项的列表有2-3项，即满足A[n].length为2或3
  - 第二阶段
    - 遍历最终列表，找出频率最高的一项，如果存在不止一个频率最高则从中随机选择一个(这里没有真的随机，具体分析见下文)
    - 我们先看这一段代码，s是最终结果，a是一个dict或者说map，它建立了列表项到其出现频率的映射
    - 这段代码遍历了最终列表的列表项，如果其不在a中则加入a，对a中的对应项，增加其频率，如果增加后的频率超过了最终结果的频率则更新最终结果
```
var a = {}, s = -1;
for (var l = 0; l < t.length; l++)
	void 0 === a[t[l]] && (a[t[l]] = 0),
	a[t[l]]++, -1 == s ? s = t[l] : a[t[l]] > a[s] && (s = t[l]);
```
    - 可以发现，如果存在不止一个频率最高，上述代码返回的是首次出现最早的而不是随机的，作者实现随机返回一个通过的是在上面代码开始执行前使用t.shuffle()随机打乱最终列表
  - 算法最终返回一个数字，作为专业结果的编号，这个对应关系同样可以在JavaScript中找到，见下面给出的表2
- 算法补充分析如下
  - 笔者在开始分析前进行了多次测试，并没有发现结果不唯一的情况，经过上述分析之后笔者构造了数据希望看到这种随机情况，采用的数据如下
```
C C A B A A B C BC A
```
  - 对这组数据很容易得到下面的最终列表，从而得出22/23/27都有最高的频率6，因此结果有高几率出现不同
```
22, 23, 24, 25, 27
5, 14, 22
1, 3, 4, 5, 9, 10, 14, 21, 22, 23, 24, 27
1, 5, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 23, 26, 27
1, 3, 4, 5, 9, 10, 14, 21, 22, 23, 24, 27
1, 0, 2, 6, 7, 8, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 23, 25, 26, 27
5, 22, 23, 24
15, 16, 17, 18, 19, 25, 27
6, 15, 13
```
  - 但经过多次测试，期待的结果不同始终没有发生，为此笔者进行了单步调试发现了问题所在，即下面这一段代码
```
(Array.prototype.shuffle = function() {
	for (var A, e, t = this.length; t; A = parseInt(Math.random() * t),
		e = this[--t],
		this[t] = this[A],
		this[A] = e)
		return this
});
```
  - 注意下面for循环的执行顺序是，执行A，执行B，若B假则跳出循环，否则执行D再执行C再执行B，若B假则跳出循环，以此类推
  - 那么对于上面的循环，先执行A也就是var A, e, t = this.length，再执行B也就是t，如果结果为真执行C也就是return this返回，等于什么都没有改变
```
for (/* [A] */; /* [B] */; /* [C] */) {
	/* [D] */
}
```
  - 所以结果出现了不同那才是见鬼，这位作者应该是漏写了for循环右括号外面的分号，不得不说这编码能力和测试能力还有待提高啊
- 给出上文提到的两个表
  - 表1(截取自上述JS)
```
0: {
	0: [1, 0, 2, 3, 4, 5, 6, 7, 8, 21, 26],
	1: [9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 26],
	2: [22, 23, 24, 25, 27]
},
1: {
	0: [0, 2, 6, 7, 20, 21, 25],
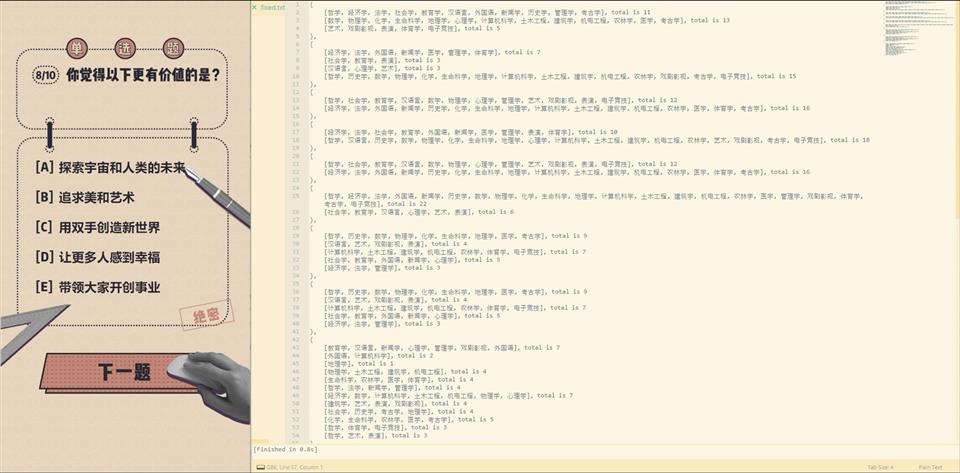
	1: [3, 4, 24],
	2: [5, 14, 22],
	3: [1, 8, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 23, 26, 27]
},
2: {
	0: [1, 3, 4, 5, 9, 10, 14, 21, 22, 23, 24, 27],
	1: [0, 2, 6, 7, 8, 11, 12, 13, 15, 16, 17, 18, 19, 20, 25, 26]
},
3: {
	0: [0, 2, 3, 4, 6, 7, 20, 21, 24, 25],
	1: [1, 5, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 23, 26, 27]
},
4: {
	0: [1, 3, 4, 5, 9, 10, 14, 21, 22, 23, 24, 27],
	1: [0, 2, 6, 7, 8, 11, 12, 13, 15, 16, 17, 18, 19, 20, 25, 26]
},
5: {
	0: [1, 0, 2, 6, 7, 8, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 23, 25, 26, 27],
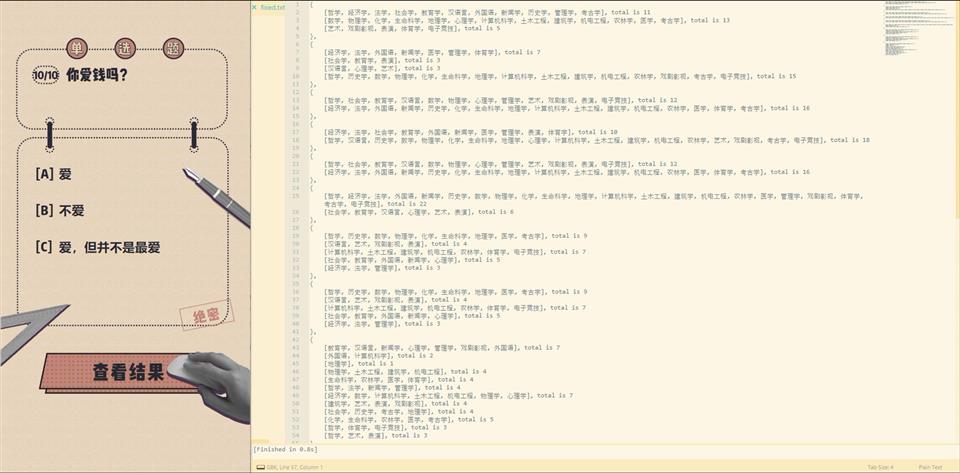
	1: [3, 4, 5, 14, 22, 24]
},
6: {
	0: [1, 8, 9, 10, 11, 12, 13, 20, 26],
	1: [5, 22, 23, 24],
	2: [15, 16, 17, 18, 19, 25, 27],
	3: [3, 4, 6, 7, 14],
	4: [0, 2, 21]
},
7: {
	0: [1, 8, 9, 10, 11, 12, 13, 20, 26],
	1: [5, 22, 23, 24],
	2: [15, 16, 17, 18, 19, 25, 27],
	3: [3, 4, 6, 7, 14],
	4: [0, 2, 21]
},
8: {
	0: [4, 5, 7, 14, 21, 23, 6],
	1: [6, 15],
	2: [13],
	3: [10, 16, 17, 18],
	4: [12, 19, 20, 25],
	5: [1, 2, 7, 21],
	6: [0, 9, 15, 16, 18, 10, 14],
	7: [17, 22, 24, 23],
	8: [3, 8, 26, 13],
	9: [11, 12, 19, 20, 26],
	10: [25, 27],
	11: [22, 24]
},
9: {
	0: [],
	1: [],
	2: []
}
```
  - 表2(截取自上述JS)
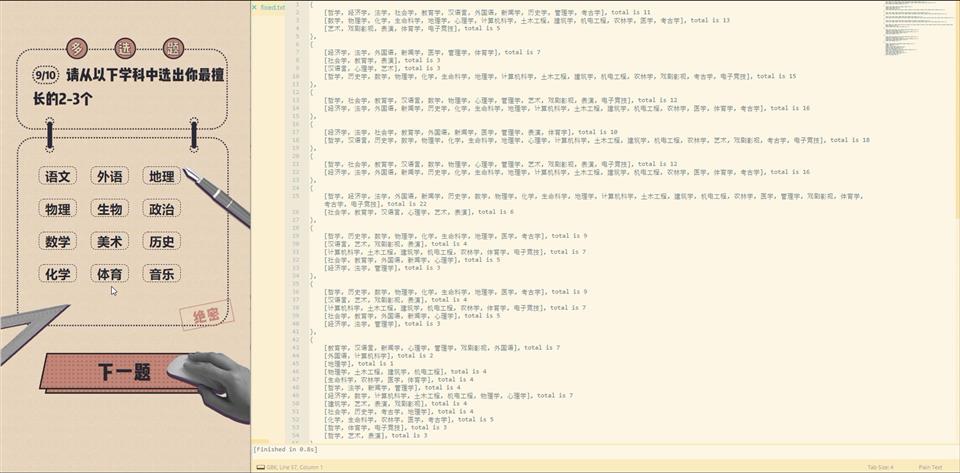
```
W = ["jingjixue", "zhexue", "faxue", "shehuixue", "jiaoyuxue", "hanyuyan", "waiguo", "xinwenxue", "lishixue", "shuxue", "wulixue", "huaxue", "shengmingkexue", "dilixue", "xinlixue", "jisuanjikexue", "tumugongcheng", "jianzhuxue", "jidiangongcheng", "nonglinxue", "yixue", "guanlixue", "yishu", "xijuyingshi", "biaoyan", "tiyuxue", "kaoguxue", "dianzijingji"],
```
- 给出直观的选项标签对应关系
  - 选项标签对应关系说明
    - 从上面给出的两个表看题目选项的对应关系是痛苦的，为此笔者使用CPP对上面的内容进行了一些格式化，直观的给出每道题目每个选项的对应关系
    - 最后一题全部选项的标签列表都是空列表，因此没有在下面的图中展示
  - 选项标签对应关系一览
  - 格式化程序的代码与一些说明
    - 映射字符数组定义如下
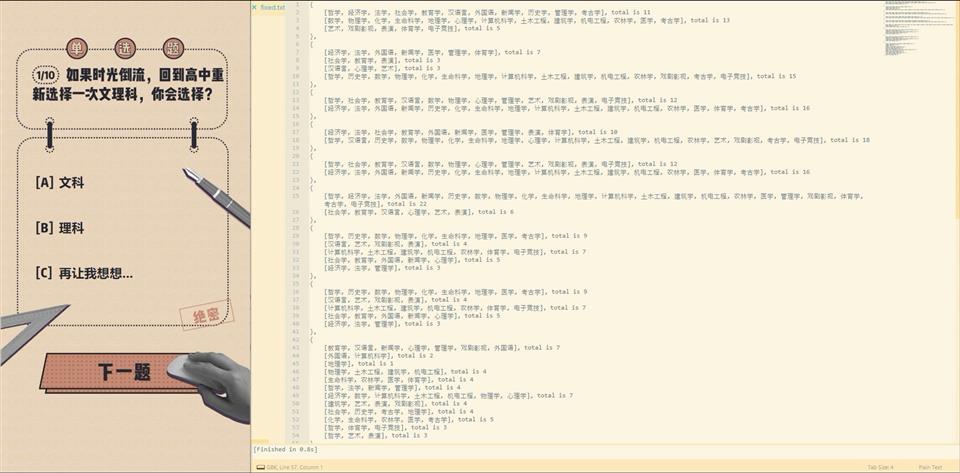
```
const char* text[]=
{
	"经济学","哲学","法学","社会学","教育学",
	"汉语言","外国语","新闻学","历史学","数学",
	"物理学","化学","生命科学","地理学","心理学",
	"计算机科学","土木工程","建筑学","机电工程","农林学",
	"医学","管理学","艺术","戏剧影视","表演",
	"体育学","考古学","电子竞技"
};
```
    - 格式化的实质是多行不定量数字输入的解析，这里手写快读来实现，s是被读取的字符数组，idx是字符数组读到的位置的引用
    - (o<<3)+(o<<1)+(c^48)其实是o*10+c-‘0‘的意思，有兴趣可以自行了解位运算
    - 由于正常读取不会读到负数，我们在读到头的时候返回负数进行区分
```
inline int read(char* s,int& idx)
{
	int o=0; char c=s[idx++];
	while (c && (c<‘0‘ || c>‘9‘)) c=s[idx++];
	while (c>=‘0‘ && c<=‘9‘)
		o=(o<<3)+(o<<1)+(c^48),c=s[idx++];
	return c?o:-1;
}
```
    - 注意到行形如2: [5, 14, 22],，按行读取的时候需要先跳过第一个数字，之后利用read读取即可，顺便可以统计读取到的数量
```
inline void solve(char* s)
{
	int i,idx=0,cnt=0;
	printf("\t[");
	read(s,idx);
	if ((i=read(s,idx))!=-1)
	{
		printf("%s",text[i]),cnt++;
		while ((i=read(s,idx))!=-1)
			printf(", %s",text[i]),cnt++;
	}
	printf("], total is %d\n",cnt);
	return;
}
```
    - 最后完成主函数，重定向输入输出后按行读取直到文件末尾，特别的，如果一行中不包含中括号，则无需处理直接输出即可
```
int main()
{
	char *s=(char*)malloc(1<<10);
	freopen("tag.txt","r",stdin);
	freopen("fixed.txt","w",stdout);
	while (fgets(s,1<<10,stdin))
	{
		if (strchr(s,‘[‘)) solve(s);
		else fputs(s,stdout);
	}
	return 0;
}
```

结果评价

直观分析
- 分析上述选项标签对应关系，可以直观的得到两个结论
- 你的性别/目前的专业对结果没有影响，没整男理女文之类的诡异操作，还是值得肯定的
- 你对钱的热爱程度对结果没有影响，~~算是个超然于金钱之外的清高作者~~
- 更多的分析就见仁见智了，笔者将不进行更多的讨论，而是采用统计的方式进行进一步的解读

统计分析

统计分析说明
- 显然选项的组合数量是有限的，且算法已知，我们可以枚举全部选项组合统计结果，观察各个专业的占比情况

给出按照原始错误算法计算出的结果

按照专业id升序排序的结果

major count percent

经济学 55896 4.07%

哲学 53735 3.91%

法学 30227 2.20%

社会学 73748 5.37%

教育学 39249 2.86%

汉语言 73436 5.35%

外国语 64519 4.70%

新闻学 43233 3.15%

历史学 33503 2.44%

数学 35957 2.62%

物理学 29806 2.17%

化学 13529 0.99%

生命科学 28147 2.05%

地理学 36290 2.64%

心理学 93522 6.81%

计算机科学 59620 4.34%

土木工程 28676 2.09%

建筑学 26632 1.94%

机电工程 0 0.00%

农林学 25619 1.87%

医学 69655 5.07%

管理学 65040 4.74%

艺术 95100 6.93%

戏剧影视 57054 4.16%

表演 82970 6.04%

体育学 89138 6.49%

考古学 28874 2.10%

电子竞技 39625 2.89%

major	count	percent
经济学	55896	4.07%
哲学	53735	3.91%
法学	30227	2.20%
社会学	73748	5.37%
教育学	39249	2.86%
汉语言	73436	5.35%
外国语	64519	4.70%
新闻学	43233	3.15%
历史学	33503	2.44%
数学	35957	2.62%
物理学	29806	2.17%
化学	13529	0.99%
生命科学	28147	2.05%
地理学	36290	2.64%
心理学	93522	6.81%
计算机科学	59620	4.34%
土木工程	28676	2.09%
建筑学	26632	1.94%
机电工程	0	0.00%
农林学	25619	1.87%
医学	69655	5.07%
管理学	65040	4.74%
艺术	95100	6.93%
戏剧影视	57054	4.16%
表演	82970	6.04%
体育学	89138	6.49%
考古学	28874	2.10%
电子竞技	39625	2.89%

按照结果占比降序排序的结果

major count percent

艺术 95100 6.93%

心理学 93522 6.81%

体育学 89138 6.49%

表演 82970 6.04%

社会学 73748 5.37%

汉语言 73436 5.35%

医学 69655 5.07%

管理学 65040 4.74%

外国语 64519 4.70%

计算机科学 59620 4.34%

戏剧影视 57054 4.16%

经济学 55896 4.07%

哲学 53735 3.91%

新闻学 43233 3.15%

电子竞技 39625 2.89%

教育学 39249 2.86%

地理学 36290 2.64%

数学 35957 2.62%

历史学 33503 2.44%

法学 30227 2.20%

物理学 29806 2.17%

考古学 28874 2.10%

土木工程 28676 2.09%

生命科学 28147 2.05%

建筑学 26632 1.94%

农林学 25619 1.87%

化学 13529 0.99%

机电工程 0 0.00%

major	count	percent
艺术	95100	6.93%
心理学	93522	6.81%
体育学	89138	6.49%
表演	82970	6.04%
社会学	73748	5.37%
汉语言	73436	5.35%
医学	69655	5.07%
管理学	65040	4.74%
外国语	64519	4.70%
计算机科学	59620	4.34%
戏剧影视	57054	4.16%
经济学	55896	4.07%
哲学	53735	3.91%
新闻学	43233	3.15%
电子竞技	39625	2.89%
教育学	39249	2.86%
地理学	36290	2.64%
数学	35957	2.62%
历史学	33503	2.44%
法学	30227	2.20%
物理学	29806	2.17%
考古学	28874	2.10%
土木工程	28676	2.09%
生命科学	28147	2.05%
建筑学	26632	1.94%
农林学	25619	1.87%
化学	13529	0.99%
机电工程	0	0.00%

给出按照修复shuffle后的算法计算出的结果

按照专业id升序排序的结果

major count percent

经济学 39508 2.88%

哲学 33830 2.46%

法学 30929 2.25%

社会学 55427 4.04%

教育学 40098 2.92%

汉语言 48557 3.54%

外国语 59138 4.31%

新闻学 51414 3.75%

历史学 19030 1.39%

数学 16750 1.22%

物理学 49155 3.58%

化学 7487 0.55%

生命科学 28192 2.05%

地理学 44696 3.26%

心理学 90569 6.60%

计算机科学 41542 3.03%

土木工程 24746 1.80%

建筑学 42353 3.09%

机电工程 24616 1.79%

农林学 38035 2.77%

医学 67257 4.90%

管理学 78235 5.70%

艺术 80525 5.87%

戏剧影视 61330 4.47%

表演 104148 7.59%

体育学 84743 6.17%

考古学 67820 4.94%

电子竞技 42670 3.11%

major	count	percent
经济学	39508	2.88%
哲学	33830	2.46%
法学	30929	2.25%
社会学	55427	4.04%
教育学	40098	2.92%
汉语言	48557	3.54%
外国语	59138	4.31%
新闻学	51414	3.75%
历史学	19030	1.39%
数学	16750	1.22%
物理学	49155	3.58%
化学	7487	0.55%
生命科学	28192	2.05%
地理学	44696	3.26%
心理学	90569	6.60%
计算机科学	41542	3.03%
土木工程	24746	1.80%
建筑学	42353	3.09%
机电工程	24616	1.79%
农林学	38035	2.77%
医学	67257	4.90%
管理学	78235	5.70%
艺术	80525	5.87%
戏剧影视	61330	4.47%
表演	104148	7.59%
体育学	84743	6.17%
考古学	67820	4.94%
电子竞技	42670	3.11%

按照结果占比降序排序的结果

major count percent

表演 104148 7.59%

心理学 90569 6.60%

体育学 84743 6.17%

艺术 80525 5.87%

管理学 78235 5.70%

考古学 67820 4.94%

医学 67257 4.90%

戏剧影视 61330 4.47%

外国语 59138 4.31%

社会学 55427 4.04%

新闻学 51414 3.75%

物理学 49155 3.58%

汉语言 48557 3.54%

地理学 44696 3.26%

电子竞技 42670 3.11%

建筑学 42353 3.09%

计算机科学 41542 3.03%

教育学 40098 2.92%

经济学 39508 2.88%

农林学 38035 2.77%

哲学 33830 2.46%

法学 30929 2.25%

生命科学 28192 2.05%

土木工程 24746 1.80%

机电工程 24616 1.79%

历史学 19030 1.39%

数学 16750 1.22%

化学 7487 0.55%

虽然使用了shuffle，导致存在随机性，但笔者进行了多次测试，除了土木工程和机电工程占比相近有一定概率顺序反转外，可以认为结果分布是固定的

major	count	percent
表演	104148	7.59%
心理学	90569	6.60%
体育学	84743	6.17%
艺术	80525	5.87%
管理学	78235	5.70%
考古学	67820	4.94%
医学	67257	4.90%
戏剧影视	61330	4.47%
外国语	59138	4.31%
社会学	55427	4.04%
新闻学	51414	3.75%
物理学	49155	3.58%
汉语言	48557	3.54%
地理学	44696	3.26%
电子竞技	42670	3.11%
建筑学	42353	3.09%
计算机科学	41542	3.03%
教育学	40098	2.92%
经济学	39508	2.88%
农林学	38035	2.77%
哲学	33830	2.46%
法学	30929	2.25%
生命科学	28192	2.05%
土木工程	24746	1.80%
机电工程	24616	1.79%
历史学	19030	1.39%
数学	16750	1.22%
化学	7487	0.55%

简要对分析程序的CPP代码实现进行一些说明

映射字符数组定义如下

const char* text[]=
{
	"经济学","哲学","法学","社会学","教育学",
	"汉语言","外国语","新闻学","历史学","数学",
	"物理学","化学","生命科学","地理学","心理学",
	"计算机科学","土木工程","建筑学","机电工程","农林学",
	"医学","管理学","艺术","戏剧影视","表演",
	"体育学","考古学","电子竞技"
};

选项标签数组定义如下，vector就是香啦

vector<vector<vector<int>>> reflect=
{
	{
		{1,0,2,3,4,5,6,7,8,21,26},
		{9,10,11,12,13,14,15,16,17,18,19,20,26},
		{22,23,24,25,27}
	},
	{
		{0,2,6,7,20,21,25},
		{3,4,24},
		{5,14,22},
		{1,8,9,10,11,12,13,15,16,17,18,19,23,26,27}
	},
	{
		{1,3,4,5,9,10,14,21,22,23,24,27},
		{0,2,6,7,8,11,12,13,15,16,17,18,19,20,25,26}
	},
	{
		{0,2,3,4,6,7,20,21,24,25},
		{1,5,8,9,10,11,12,13,14,15,16,17,18,19,22,23,26,27}
	},
	{
		{1,3,4,5,9,10,14,21,22,23,24,27},
		{0,2,6,7,8,11,12,13,15,16,17,18,19,20,25,26}
	},
	{
		{1,0,2,6,7,8,9,10,11,12,13,15,16,17,18,19,20,21,23,25,26,27},
		{3,4,5,14,22,24}
	},
	{
		{1,8,9,10,11,12,13,20,26},
		{5,22,23,24},
		{15,16,17,18,19,25,27},
		{3,4,6,7,14},
		{0,2,21}
	},
	{
		{1,8,9,10,11,12,13,20,26},
		{5,22,23,24},
		{15,16,17,18,19,25,27},
		{3,4,6,7,14},
		{0,2,21}
	},
	{
		{4,5,7,14,21,23,6},
		{6,15},
		{13},
		{10,16,17,18},
		{12,19,20,25},
		{1,2,7,21},
		{0,9,15,16,18,10,14},
		{17,22,24,23},
		{3,8,26,13},
		{11,12,19,20,26},
		{25,27},
		{22,24}
	}
};

定义结果类，包含两个类属性和三个对象属性
两个类属性分别是搜索到的总结果数和28个专业对应结果的个数，初始化为0
三个对象属性分别是前八题的结果，第九题的结果数量和结果
pushUp方法在搜索完成后被调用，根据三个对象属性计算结果，并更新两个类属性

值得注意的是CPP提供了shuffle函数，无需我们自行实现

class Ans
{
public:
	static int total;
	static int summary[28];
	int cnt,last[3],normal[8];

	inline void pushUp()
	{
		vector<int> temp;
		if (++total%50000==0) printf("%07d searched\n",total);
		for (int i=0;i<(int)(sizeof(normal)/sizeof(*normal));i++)
			for (vector<int>::iterator it=reflect[i][normal[i]].begin();
				it!=reflect[i][normal[i]].end();it++)
				temp.push_back(*it);
		for (int i=0;i<cnt;i++)
			for (vector<int>::iterator it=reflect[reflect.size()-1][last[i]].begin();
				it!=reflect[reflect.size()-1][last[i]].end();it++)
				temp.push_back(*it);
		if (SHUFFLE) shuffle(temp.begin(),temp.end(),generator);
		int out=-1,vis[28]={0};
		for (int i=0;i<(int)temp.size();i++)
		{
			vis[temp[i]]++;
			if (out==-1) out=temp[i];
			else if (vis[temp[i]]>vis[out]) out=temp[i];
		}
		summary[out]++;
		return;
	}
};

int Ans::total=0;
int Ans::summary[28]={0};

实现搜索函数，传入当前搜索下标，最大下标和Ans对象的指针

第九题的处理采用分别二层循环和三层循环的偷懒方式，如果允许多选的数量更多，再套一个dfs搜一下组合即可

void dfs(int cur,int top,Ans* ans)
{
	if (cur==top)
	{
		int range=reflect[reflect.size()-1].size();
		ans->cnt=2;
		for (int i=0;i<range;i++)
			for (int j=i+1;j<range;j++)
			{
				ans->last[0]=i;
				ans->last[1]=j;
				ans->pushUp();
			}
		ans->cnt=3;
		for (int i=0;i<range;i++)
			for (int j=i+1;j<range;j++)
				for (int k=j+1;k<range;k++)
				{
					ans->last[0]=i;
					ans->last[1]=j;
					ans->last[2]=k;
					ans->pushUp();
				}
		return;
	}
	for (int i=0;i<(int)reflect[cur].size();i++)
	{
		ans->normal[cur]=i;
		dfs(cur+1,top,ans);
	}
	return;
}

定义结果分析类管理专业id，专业数量和专业占比

重载两个比较运算符用于排序，实现两个输出方法用于正常输出和MarkDown表格格式的输出

class Node
{
public:
	int idx,val;
	double percent;

	inline Node(int idx,int val,int total)
	{
		this->idx=idx,this->val=val;
		percent=1.0*val/total*100;
		return;
	}

	inline void print() const
	{
		printf("major = %-10s  |  count = %06d  |  percent = %5.2lf%%\n",
			text[idx],val,percent);
		return;
	}

	inline void toMarkDown() const
	{
		printf("| %s | %d | %5.2lf%% |\n",
			text[idx],val,percent);
		return;
	}

	inline bool operator>(Node& rhs) const
	{
		return this->val<rhs.val;
	}

	inline bool operator<(Node& rhs) const
	{
		return this->val>rhs.val;
	}
};

完成主函数，搜出全部结果后统计分析并输出一次，按百分比排序后再输出一次即可

int main()
{
	Ans ans;
	puts("----- search started -----\n");
	dfs(0,sizeof(ans.normal)/sizeof(*ans.normal),&ans);
	printf("\n----- search finished, total = %d, analysing -----\n\n",Ans::total);
	vector<Node> analyse;
	for (int i=0;i<(int)(sizeof(Ans::summary)/sizeof(*Ans::summary));i++)
	{
		printf("%02d / %d done\n",i,(int)(sizeof(Ans::summary)/sizeof(*Ans::summary)));
		Node node(i,Ans::summary[i],Ans::total);
		analyse.push_back(node);
	}
	if (MARKDOWN) puts("| major | count | percent |\n| :---: | :---: | :---: |");
	else puts("\n----- result sort by major id -----\n");
	for (vector<Node>::iterator it=analyse.begin();it!=analyse.end();it++)
		if (MARKDOWN) it->toMarkDown();
		else it->print();
	sort(analyse.begin(),analyse.end());
	if (MARKDOWN) puts("| major | count | percent |\n| :---: | :---: | :---: |");
	else puts("\n----- result sort by percent -----\n");
	for (vector<Node>::iterator it=analyse.begin();it!=analyse.end();it++)
		if (MARKDOWN) it->toMarkDown();
		else it->print();
	return 0;
}

最后，这个计算量还是有一些的，为了获得更好的体验，可以吸两口氧
```
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
```

结语
- 这个小测试和上次的网易云一样，都采用了打标签的形式，这种形式躲不开的一点就是多个标签数量相同的处理，个人认为衡量这类测试的靠谱程度很重要的一点就是这里，笔者不认为任何形式的随机(如这次作者想实现还写错了的打乱，网易云的遍历HashMap带来的随机)是靠谱和对用户负责的，换句话说结果必须是确定的
- 对于多个标签数量相同的处理，个人想到的一种处理是设置优先级，给出多个相同标签中优先级最高的作为结果，当然打标签并不是这种小测试唯一的实现思路，下次笔者将选择一个不基于打标签的小测试进行分析和解读和一些拓展
- 分析这些小测试还是挺有趣也挺有收获的，过程中包括HTML/CSS/JS，Network/抓包/爬虫，CPP/Java/Python在内的能力都得到了或多或少的锻炼
- 送给看到这里的2021高考的学弟学妹们，计算机超有趣的，如果不确定选什么专业的话，计算机也是个不错的选择哦

对本命专业测试算法与结果分布的简要分析

原文：https://www.cnblogs.com/Chenrt/p/14912590.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)

对本命专业测试算法与结果分布的简要分析

对本命专业测试算法与结果分布的简要分析

测试过程

PC浏览器打开

Network分析

寻找JavaScript

算法解析

算法完整代码如下

算法流程描述如下

第一阶段

第二阶段

算法补充分析如下

给出上文提到的两个表

表1(截取自上述JS)

表2(截取自上述JS)

给出直观的选项标签对应关系

选项标签对应关系说明

选项标签对应关系一览

格式化程序的代码与一些说明

结果评价

直观分析

统计分析

统计分析说明

给出按照原始错误算法计算出的结果

给出按照修复shuffle后的算法计算出的结果

简要对分析程序的CPP代码实现进行一些说明

结语