Java数字类型隐式转换

隐式转换关系

精度丢失

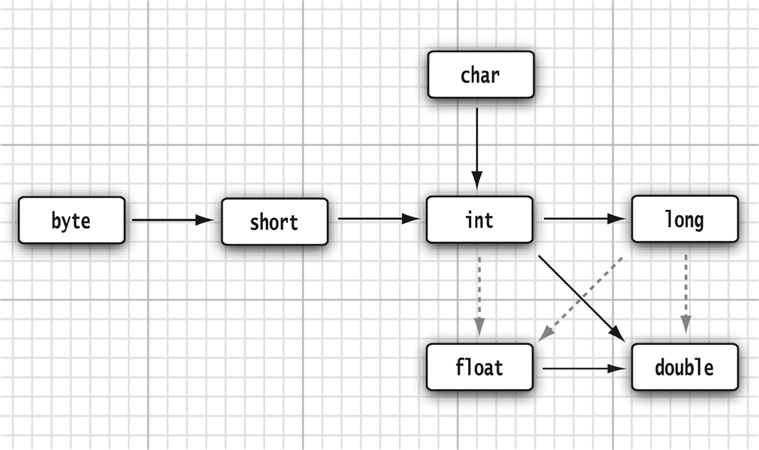
上图中虚线表示转换过程中存在精度丢失问题，因为与其它数据类型的十进制直接转换为二进制不同，float、double有其独特的数据结构，如下所示：

float举例分析

以float为例进行分析，例如：12.15623，执行以下步骤：

1. 对整数位转化为二进制：除二取余，倒序排列，即整数依次除二直到商为0或1的时候结束，然后将余数倒序写出，不足位高位补0

12/2    0   低位
6/2     0
3/2     1
1/2     1   高位
12 = 0000 1100B

2. 对小数位转换为二进制：乘二取整，顺序排列，即小数位*2，取计算结果的整数位排列，直到小数部分为0，不足位进行低位补0

0.15623*2 = 0.31246   0
0.31246*2 = 0.62492   0
0.62492*2 = 1.24984   1
0.24984*2 = 0.49968   0
0.49968*2 = 0.99936   0
0.99936*2 = 1.99872   1
0.99872*2 = 1.99744   1
0.99744*2 = 1.99488   1 
...
0.15623 = 0.00100111111111101011000001110100101001110111001

存在无限循环或者小数位过多的情况，例如：float尾数位23bit表示，这也是浮点数无法精确表示的原因之一

3. 12.15623的完整二进制为：1100.00100111...，可通过在线进制转换验证
4. 根据IEEE 754标准，其实际表示形式为：$ v = (-1)^{sign} \times M \times 2^E $

• M：尾数，M = 1 + f，其中$ 0 \le f < 1 \(，f的二进制表示为\) 0.f_{n-1}...f_1f_0 \(，因此M的二进制可以看做是\) 1.f_{n-1}...f_1f_0 \(，可通过对12.15623的二进制进行位移使尾数M的范围保持在\) 1 \le M <2 $，向右移3位变为：1.10000100111...。实际就是转化为二进制科学计数，由于尾数最高位总是为1，所以高位直接隐去，12.15623的尾数即为10000100111111111101011，float用23位表示，double用52位表示，所以才有了精度的不同
• E：指数，E = 位移数(右移取整数，反之取负数，也可以理解为二进制计数法的指数) + 127，因此，12.15623的指数E = 3 + 127 = 130，转化为二进制为：10000010。float指数位有8位，但实际指数需要减去127，也就是$ 2^7 $ = 128，所以float的最大范围是$ -2^{128} \sim 2^{128} $
• 根据float的存储结构：1位符号位+8位指数位+23位尾数位，12.15623实际存储为：
  \(\color{#4285f2}{0}\color{#ea4335}{1000001}\quad\color{#ea4335}{0}\color{#34a853}{1000010}\quad\color{#34a853}{01111111}\quad\color{#34a853}{11101011}\)

结果验证

反向推导

\(\color{#4285f2}{0}\color{#ea4335}{1000001}\quad\color{#ea4335}{0}\color{#34a853}{1000010}\quad\color{#34a853}{01111111}\quad\color{#34a853}{11101011}\)

• 尾数M高位为1，补1后 = 1.1000010 01111111 11101011
• 指数E = 1000 0010B = 130，位移数 = 130 -127 = 3
• 实际尾数M左移3位即为实际二进制： 1100.0010 01111111 11101011
• 二进制转换为十进制，过程如下：
  \(12+(1/8+1/64+1/128+1/256+1/512+1/1024+1/2048+1/4096+1/8192+1/16384+1/32768+1/131072+1/524288+1/1048576)\)
  \(value = 12+0.15622997283935547 = 12.15622997283935547\)

公式推导

\(value = (-1)^{sign} \times (1+\sum_{i=1}^{23} b_{23-i}2^{-i})\times2^{e-127}\)

求和展开后如下：

\(value = (-1)^{sign} \times (1+b_{22}2^{-1}+b_{21}2^{-2}+...+b_{0}2^{-23}) \times2^{e-127}\)

其中\(b_n2^{n-23}\)，当尾数位为0时结果都是0，可直接忽略。因此，尾数位求和只取尾数位等于1的即可。\(\color{#4285f2}{0}\color{#ea4335}{1000001}\quad\color{#ea4335}{0}\color{#34a853}{1000010}\quad\color{#34a853}{01111111}\quad\color{#34a853}{11101011}\)代入公式为：

\(value = (-1)^0 \times (1+2^{-1}+2^{-6}+2^{-9\sim-18}+2^{-20}+2^{-22}+2^{-23}) \times2^{130-127}\)

\(value = 1 \times (1+1/2+1/64+1/512+1/1024+1/2048+1/4096+1/8192+1/16384+1/32768+1/65536+1/131072+1/262144+1/1048576+1/4194304+1/8388608) \times2^3\)

\(value = 1 \times 1.5195287466049194 \times 8 = 12.156229972839355\)

精度的计算

还是以float举例，尾数一共23位，加上隐藏位1，实际有24位，所能表示的取值范围\([0,2^{24}-1]\)，最大值为16777215，转化为二进制科学计数法为\(1.1111111 11111111 1111111 * 2^{23}\)。比这个大的数小数位已经是24位了，存储时超出的位数就被舍弃掉了。因此，可以得出以下结论：

• 小于16777215的整数都可以精确表示
• 小于16777215的非整数可能不能精确表示，因为小数转化为二进制位数不能保证，且可能存在无限循环的情况。如果是是16777215以内的整数乘以\(2^{-n}\)即可精确表示。例如：（16777214*1/2048=8191.9990234375，其二进制为\(1.1111111111111111111111*2^{12}\)，存储不会出现精度丢失，但是java中打印为：8191.999，默认显示8位）
• 超出16777215的整数可能不能精确表示，即存在可以精确表示的。如果刚好是\(2^n\)，或者是16777215以内的整数乘以\(2^n\)，这样超出的位数都是0，例如：33554432其二进制科学计数法为\(1.0000000 00000000 00000000*2^{25}\)
• 超出16777215的非整数不能精确表示，小数位肯定被丢弃了

最终结论：精度是由尾数的位数来决定的，浮点数在内存中是按科学计数法来存储的，其整数部分始终是1，由于它是不变的，故不能对精度造成影响。数学领域的精度一般指有效位数，即十进制位数。因此，结论如下：

• float：2^23 = 8388608，一共七位，最多能有7位有效数字，能绝对保证前6位，第7位可能存在舍入的情况，即float的精度为6~7位有效数字
• double：2^52 = 4503599627370496，一共16位，同理，double的精度为15~16位

疑问

印象中float的整数位+小数位一共8位，例如：

- (float)10/3=3.3333333
- (float)1/3=0.33333334

再看以下代码：

System.out.println(0.100000024f);
System.out.println(0.100000025f);
System.out.println(0.100000026f);
System.out.println(0.100000027f);
System.out.println(0.100000028f);

输出结果如下：

0.100000024
0.100000024
0.100000024
0.100000024
0.10000003

0.100000024~0.100000027输出都是0.100000024，小数位9位，0.100000028就变成0.10000003，小数位8位，为什么？？

1. 先转化为对应的二进制：

0.100000024=0.000110011001100110011010000 00000101011011110000100001011
0.100000025=0.000110011001100110011010000 00100111110010110010000000101
0.100000026=0.000110011001100110011010000 01001010001001110011011111111
0.100000027=0.000110011001100110011010000 01101100100000110100111111001
0.100000028=0.000110011001100110011010000 10001110110111110110011110011

2. 再二进制科学计数法：

• 0.100000024=1.10011001100110011010000*\(2^{-4}\)
• 0.100000025=1.10011001100110011010000*\(2^{-4}\)
• 0.100000026=1.10011001100110011010000*\(2^{-4}\)
• 0.100000027=1.10011001100110011010000*\(2^{-4}\)
• 0.100000028=1.10011001100110011010001*\(2^{-4}\)

由于尾数位只有23位，丢弃多余部分，0.100000024~0.100000027的数据结构完全一样，0.100000028由于第24位是1，舍弃时进位使23位变成了1，这就是差异部分

3. 代入上文中公式：

0.100000024如下：
\((1+1/2+1/16+1/32+1/256+1/512+1/4096+1/8192+1/65536+1/131072+1/524288)*2^{-4}=0.10000002384185791\)
0.100000028如下：
\((1+1/2+1/16+1/32+1/256+1/512+1/4096+1/8192+1/65536+1/131072+1/524288+1/8388608)*2^{-4}=0.10000003129243851\)

到这一步，可以看出其不同，但为什么输出0.100000024和0.10000003呢？

观察结果如下：

• 0.10000002384185791比原数小，多取一位进行四舍五入，更接近原值
• 0.10000003129243851已经比原值大了，默认取8位，丢弃多余的位数
• 还是一种是上文提到的8191.9990234375打印输出为8191.999，可以精确表示，但是默认也只输出8位

结论：

• 精度是指有效数字，和小数位的多少没有必然联系，小数位是不定的
• float默认显示的小数位并不代表其实际精度

Java数字类型隐式转换

原文：https://www.cnblogs.com/sheung/p/14888429.html