565，多种方式解2的幂

Yesterday is history, tomorrow is a mystery. But today is a gift.?

昨日已成往事，未来还未可知。但是今天是上天的馈赠。

问题描述

来源：LeetCode第231题

难度：简单

?

给你一个整数n，请你判断该整数是否是2的幂次方。如果是，返回true；否则，返回false。

?

如果存在一个整数x使得n==2^x，则认为n是2的幂次方。

?

示例 1：

输入：n = 1

输出：true

解释：2^0 = 1

示例 2：

输入：n = 16

输出：true

解释：2^4 = 16

示例 3：

输入：n = 3

输出：false

示例 4：

输入：n = 4

输出：true

示例 5：

输入：n = 5

输出：false

?

提示：

• -2^31 <= n <= 2^31 - 1

?

递归解决

这题让判断一个数是否是2的幂次方，来看一下2的幂次方函数图像，可以看到2的幂次方一定是大于0的。

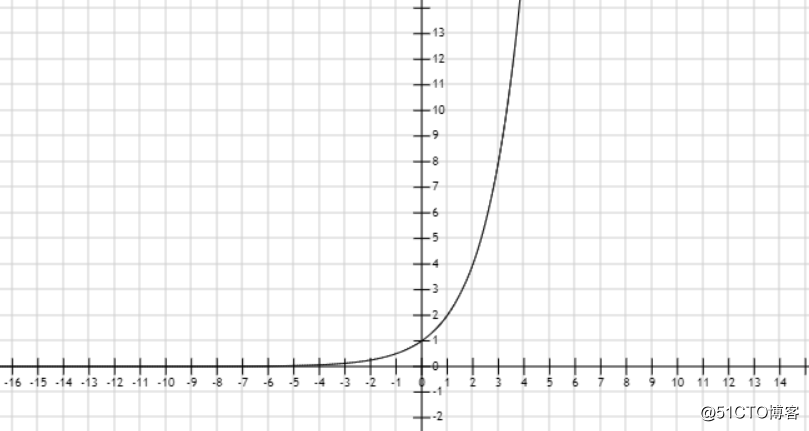
因为题中说了n和x都是整数，那么n如果是2的幂次方，他只能是2^0，2^1，2^2,……2^31。所以很容易想到的就是判断n是否是偶数，如果是偶数就一直除以2，直到是奇数为止，最后在判断这个奇数是否等于1，如果等于1返回true，否则返回false，比如8→4→2→1。代码如下

 1public?boolean?isPowerOfTwo(int?n)?{
 2????//非正数不可能是2的幂，直接返回false
 3????if?(n?<=?0)
 4????????return?false;
 5????//如果是偶数就一直除以2，直到不是偶数为止
 6????while?(n?%?2?==?0)
 7????????n?/=?2;
 8????//判断是否等于1
 9????return?n?==?1;
10}

?

位运算解决

通过上面分析我们知道，因为n和x都是整数，如果n是2的幂次方，那么n就只能是1，2，4，8，16……这样的数字。其实这些数字都有一个特点。

?

• 1的二进制位中只有一个1

• 2是1往左移一位，所以他也只有一个1
  

• 4是2往左移一位，所以他也只有一个1
  

• 8是4往左移一位，所以他也只有一个1

• ……

?

所以一个数的二进制位中如果只有一个1（符号位不算），那么这个数肯定是2的幂次方，前面我们讲过《425，剑指 Offer-二进制中1的个数》，列出了18种解法，我们可以随便找一种修改一下就是今天这题的答案，比如我们就拿第一种来修改一下，代码如下

 1public?boolean?isPowerOfTwo(int?n)?{
 2????//首先要保证n是大于0的，然后再判断n的
 3????//二进制位中1的个数是否等于1
 4????return?n?>?0?&&?hammingWeight(n)?==?1;
 5}
 6
 7//二进制中1的个数
 8public?int?hammingWeight(int?n)?{
 9????int?count?=?0;
10????for?(int?i?=?0;?i?<?32;?i++)?{
11????????if?(((n?>>>?i)?&?1)?==?1)?{
12????????????count++;
13????????}
14????}
15????return?count;
16}

在425题中讲到第5种解法（具体可以看下《364，位1的个数系列（一）》）的时候，我们知道n&(n-1)实际上就是消去n的二进制位中最右边的1，如果n的二进制位中只有一个1，那么n&(n-1)的结果肯定是0，所以我们只需要判断n大于0的时候，n&(n-1)是否等于0即可，一行代码搞定。

1public?boolean?isPowerOfTwo(int?n)?{
2????return?n?>?0?&&?(n?&?(n?-?1))?==?0;
3}

如果对位运算比较熟悉的同学应该能明白n和-n在二进制位中的区别，因为-n是n每一个都取反然后再加上1的结果，所以n和-n的区别就是n原来右边第一个1以及他右边的都不变，其他各位都是取反，具体我们来看下

• ?

public static void main(String args[]) {    System.out.println("8的二进制：" + Util.bitInt32(8));    System.out.println("-8的二进制：" + Util.bitInt32(-8));    System.out.println();    System.out.println("50的二进制：" + Util.bitInt32(50));    System.out.println("-50的二进制：" + Util.bitInt32(-50));    System.out.println();    System.out.println("24的二进制：" + Util.bitInt32(24));    System.out.println("-24的二进制：" + Util.bitInt32(-24));}

我们来看一下打印结果

所以对于这道题来说，如果n是2的幂次方，在确定n大于0的情况下，只需要判断(n&-n)==n即可，也是一行代码搞定

1public?boolean?isPowerOfTwo(int?n)?{
2????return?n?>?0?&&?(n?&?-n)?==?n;
3}

其实还有一种数学的方式，题中给出的条件是-2^31 <= n <= 2^31 - 1，所以我们可以找出在int范围类最大的2的幂次方，然后再判断这个数是否能被n整除

1public?boolean?isPowerOfTwo(int?n)?{
2????return?n?>?0?&&?Math.pow(2,?31)?%?n?==?0;
3}

?

●556，位运算解形成两个异或相等数组的三元组数目

●512，反转二进制位

●499，位运算解只出现一次的数字 III

●494，位运算解只出现一次的数字

?

?

截止到目前我已经写了500多道算法题了，为了方便大家阅读，我把部分算法题整理成了pdf文档，目前有1000多页，大家可以在公众号中回复关键字“pdf”即可获取下载链接。

?

565，多种方式解2的幂

原文：https://blog.51cto.com/u_4774266/2884037