找零兑换问题的动态规划解法

动态规划算法思路

接上一篇找零兑换问题的递归解法，找零兑换的动态规划算法：

• 从最简单的“1分钱找零”的最优解开始，逐步递加上去，直到我们需要的找零钱数；
• 在找零递加的过程中，设法保持每一分钱的递加都是最优解，一直加到求解找零钱数，自然得到最优解；
• 递加的过程能保持最优解的关键是，其依赖于更少钱数最优解的简单计算，而更少钱数的最优解已经得到了；
• 问题的最优解包含了更小规模子问题的最优解，这是一个最优化问题能够用动态规划策略解决的必要条件。
• originalamount找零兑换问题具体来说就是：

举例：11分钱的兑换问题

从一分钱兑换开始，逐步建立一个兑换表：

11分钱的兑换法步骤如下：

1. 减去1分硬币，剩下10分钱查表最优解是1
2. 减去5分硬币，剩下6分钱查表最优解是2
3. 减去10分硬币，剩下1分钱查表最优解是1
   因此，11分钱的兑换最优解是1+1=2个硬币。

动态规划解法代码：

def dpMakeChange(coinValueList, change, minCoins):
    # 从1分开始到change逐个计算最少硬币数
    for cents in range(1, change + 1):
        # 1. 初始化一个最大值
        coinCount = cents
        # 2. 减去每个硬币，向后查最少硬币数
        for j in [c for c in coinValueList if c <= cents]:
            if minCoins[cents - j] + 1 < coinCount:
                coinCount = minCoins[cents - j] + 1
        # 3. 得到当前最少硬币数，记录到表中
        minCoins[cents] = coinCount
    # 返回最后一个结果
    return minCoins[change]

print(dpMakeChange([1, 5, 10, 21, 25], 11, [0] * 12))
print(dpMakeChange([1, 5, 10, 21, 25], 63, [0] * 64))

运行代码可以得到找零11和63（贪心策略失效）的结果为2,3

动态规划算法扩展

注意：dpMakeChange并不是递归函数，是从递归算法出发得到的更高效算法
动态规划中最主要的思想是：
从最简单情况开始到达所需找零的循环其每一步都依靠以前的最优解来得到本步骤的最优解，直到得到答案。
扩展算法的目的是返回最优解的硬币组合：

1. 在生成最优解列表的同时跟踪记录所选择的硬币币值
2. 在得到最优解后，减去选择的硬币币值，回溯到表格之前的部分找零，逐步得到每一步的硬币币值

扩展代码

def dpMakeChange(coinValueList, change, minCoins, coinsUsed):
    # 从1分开始到change逐个计算最少硬币数
    for cents in range(1, change + 1):
        # 1. 初始化一个最大值
        coinCount = cents
        # 2. 初始化一下新加硬币
        newCoin = 1
        # 3. 减去每个硬币，向后查最少硬币数
        for j in [c for c in coinValueList if c <= cents]:
            if minCoins[cents - j] + 1 < coinCount:
                coinCount = minCoins[cents - j] + 1
                newCoin = j # 对应最小数量 所减的硬币
        # 4. 得到当前最少硬币数，记录到表中
        minCoins[cents] = coinCount
        coinsUsed[cents] = newCoin
    # 返回最后一个结果
    return minCoins[change]

def printCoins(coinsUsed, change):
    coin = change
    while coin > 0:
        thisCoin = coinsUsed[coin]
        print(thisCoin)
        coin = coin - thisCoin

amnt = 63
clist = [1, 5, 10, 21, 25]
coinsUsed = [0] * (amnt + 1)
coinCount = [0] * (amnt + 1)

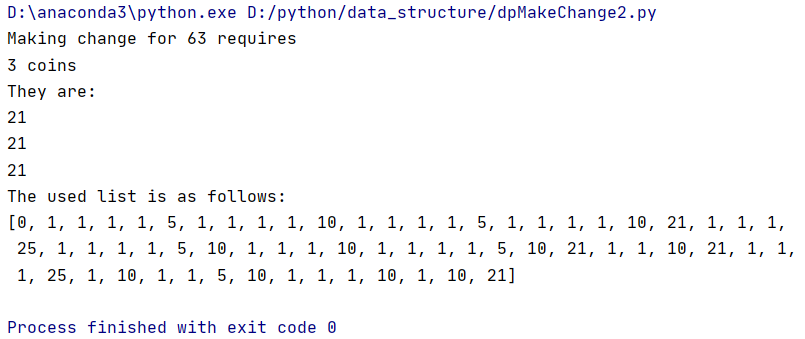
print("Making change for", amnt, "requires")
print(dpMakeChange(clist, amnt, coinCount, coinsUsed), "coins")
print("They are:")
printCoins(coinsUsed, amnt)
print("The used list is as follows:")
print(coinsUsed)

运行结果如下：

找零兑换问题的动态规划解法

原文：https://www.cnblogs.com/ikventure/p/14860866.html