NDT全称Normal Distributions Transform(正态分布变换),用来计算不同点云之间的旋转平移关系,和ICP功能类似,并且该算法能够写出多线程版本,因此速度可以比较快。
算法步骤如下,以二维点云为例:
1. 比如我们有两组点云A和B,A是固定点云,我们要把B转换到和A对齐,就要计算出B到A的旋转矩阵R和平移矩阵T,对应的就是三个参数(x,y,theta)。
2. 首先对A进行栅格化,计算每个栅格中的点云的均值和方差,记为和u和∑。
3. 设定损失函数,其中x为待匹配点云(就是上面的B点云),n为x点云总个数,损失函数记为:
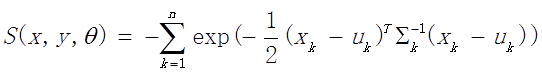
4. 要计算损失函数S达到最小时的x,y和theta,用高斯牛顿迭代求解。
5. 计算S对x,y,theta的一阶偏导,其中p就代表(x,y,theta):

6. 计算S对x,y,theta的二阶偏导,即黑塞矩阵:
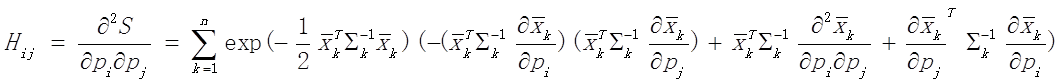
7. 设定迭代次数或者迭代阈值,计算delta=-inv(H)*g,得到迭代步长。
8. 更新参数p = p+delta,最后达到设定阈值或迭代次数即可。
matlab代码如下:
clear all;close all;clc; %生成原始点集 X=[];Y=[]; for i=-180:2:180 for j=-90:2:90 x = i * pi / 180.0; y = j * pi / 180.0; X =[X,cos(y)*cos(x)]; Y =[Y,sin(y)*cos(x)]; end end P=[X(1:3000)‘ Y(1:3000)‘]; %生成变换后点集 theta=0.5; R=[cos(theta) -sin(theta);sin(theta) cos(theta)]; X=(R*P‘)‘ + [2.4,3.5]; plot(P(:,1),P(:,2),‘b.‘); hold on; plot(X(:,1),X(:,2),‘r.‘); meanP = mean(P); meanX = mean(X); P = P - meanP; %统一起始点,否则两组点云间可能没有交集,算法会失效 X = X - meanX; minx = min(X(:,1)); miny = min(X(:,2)); maxx = max(X(:,1)); maxy = max(X(:,2)); cellsize = 0.3; %网格大小 M = floor((maxx - minx)/cellsize+1); N = floor((maxy - miny)/cellsize+1); grid = cell(M,N); meanGrid = zeros(2,M,N); convGrid = zeros(2,2,M,N); for i = 1:length(X) %划分网格并填入数据 m = floor((X(i,1) - minx)/cellsize + 1); n = floor((X(i,2) - miny)/cellsize + 1); grid{m,n} = [grid{m,n};X(i,:)]; end %计算每个网格中的均值和方差 for i=1:M for j=1:N if(size(grid{i,j},1)>=2) meanGrid(:,i,j) = mean(grid{i,j}); convGrid(:,:,i,j) = cov(grid{i,j}); end end end pre =zeros(3,1); for i=1:40 %迭代40次 g = zeros(3,1); H = zeros(3,3); tx = pre(1); ty = pre(2); theta = pre(3); for j=1:length(P) x = P(j,1); y = P(j,2); p_trans = [x*cos(theta)-y*sin(theta)+tx;x*sin(theta)+y*cos(theta)+ty]; m = floor((p_trans(1) - minx)/cellsize + 1); n = floor((p_trans(2) - miny)/cellsize + 1); if m>=1 && n>=1 && m<=M && n<=N %只计算投影到网格中的点云数据 if (size(grid{m,n},1)>=2) q = meanGrid(:,m,n); sigma = convGrid(:,:,m,n); if(cond(sigma)>50) %根据矩阵条件数判断是否是病态矩阵 continue; end invsigma = inv(sigma); xk = p_trans - q; dx = [1;0]; dy = [0;1]; dt = [-x*sin(theta)-y*cos(theta);x*cos(theta)-y*sin(theta)]; ddt = [-x*cos(theta)+y*sin(theta);-x*sin(theta)-y*cos(theta)]; g(1) = g(1) + (xk‘*invsigma* dx *exp(-0.5*xk‘*invsigma*xk)); %计算损失函数对x的偏导 g(2) = g(2) + (xk‘*invsigma* dy *exp(-0.5*xk‘*invsigma*xk)); %计算损失函数对y的偏导 g(3) = g(3) + (xk‘*invsigma* dt *exp(-0.5*xk‘*invsigma*xk)); %计算损失函数对theta的偏导 %计算黑塞矩阵,分别计算损失函数对x,y,theta的二阶偏导 H(1,1) = H(1,1) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dx)*(xk‘*invsigma*dx)+(dx‘*invsigma*dx)); H(1,2) = H(1,2) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dx)*(xk‘*invsigma*dy)+(dx‘*invsigma*dy)); H(1,3) = H(1,3) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dx)*(xk‘*invsigma*dt)+(dx‘*invsigma*dt)); H(2,1) = H(2,1) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dy)*(xk‘*invsigma*dx)+(dy‘*invsigma*dx)); H(2,2) = H(2,2) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dy)*(xk‘*invsigma*dy)+(dy‘*invsigma*dy)); H(2,3) = H(2,3) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dy)*(xk‘*invsigma*dt)+(dy‘*invsigma*dt)); H(3,1) = H(3,1) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dt)*(xk‘*invsigma*dx)+(dt‘*invsigma*dx)); H(3,2) = H(3,2) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dt)*(xk‘*invsigma*dy)+(dt‘*invsigma*dy)); H(3,3) = H(3,3) + exp(-0.5*xk‘*invsigma*xk)*(-(xk‘*invsigma*dt)*(xk‘*invsigma*dt)+(dt‘*invsigma*dt) + xk‘*invsigma*ddt); end end end %高斯牛顿迭代求解 delta = -H\g; pre = pre + delta; end pre theta=pre(3); R=[cos(theta) -sin(theta);sin(theta) cos(theta)]; %画出变换后的点云 XX=(R*P‘)‘ + [pre(1),pre(2)] + meanX; plot(XX(:,1),XX(:,2),‘g.‘); axis equal; legend(‘原始点云‘,‘变换后点云‘,‘配准点云‘)
下面给一个用matlab自带函数计算的例子:
clear all;close all;clc; %生成原始点集 X=[];Y=[]; for i=-180:2:180 for j=-90:2:90 x = i * pi / 180.0; y = j * pi / 180.0; X =[X,cos(y)*cos(x)]; Y =[Y,sin(y)*cos(x)]; end end P=[X(1:3000)‘ Y(1:3000)‘]; %生成变换后点集 theta=-0.5; R=[cos(theta) -sin(theta);sin(theta) cos(theta)]; X=P*R + [2.4,3.5]; plot(P(:,1),P(:,2),‘b.‘); hold on; plot(X(:,1),X(:,2),‘r.‘); P = [P zeros(length(P),1)]; X = [X zeros(length(X),1)]; moving = pointCloud(P); fixed = pointCloud(X); gridStep = 0.3; tform = pcregisterndt(moving,fixed,gridStep); R = tform.Rotation; T = tform.Translation; XX=P*R + T; plot(XX(:,1),XX(:,2),‘g.‘); axis equal legend(‘原始点云‘,‘变换后点云‘,‘配准点云‘)
结果如下:
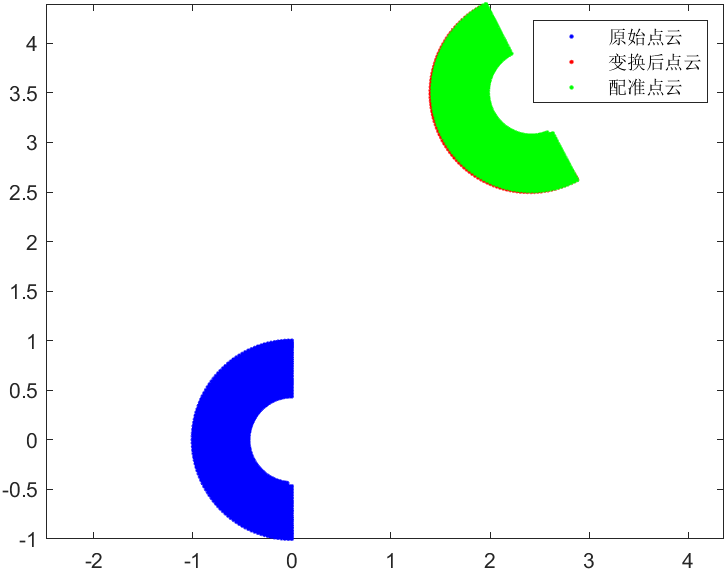
原文:https://www.cnblogs.com/tiandsp/p/14854605.html