图

目录

1. 图的存储
2. 图的遍历
3. 生成树
4. 最短路径
5. 疑难问题

图的存储

有向图

无向图

邻接矩阵

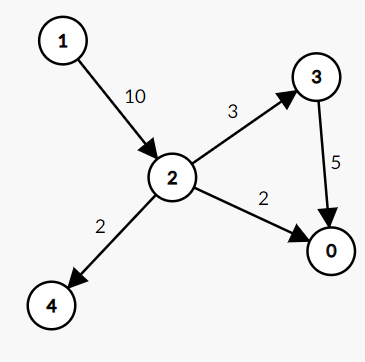
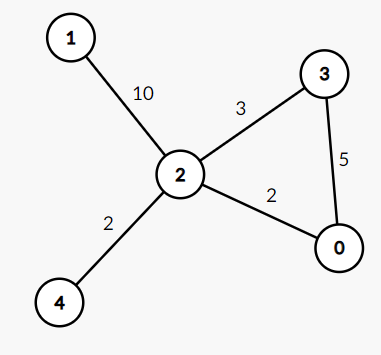
利用矩阵的方式存储图，其中无向图是关于对角线对称的。

邻接表

以链表的方式存储图。

边集数组

通常存有向图，用begin存边的开始点，end存末尾点，weight存权值。

图的遍历

DFS(深度优先)

其类似与栈，从一个点开始，一直入栈其子节点，并用visited数组记录其是否访问过。

int visited[MAXNUM]={0};         //定义visited数组记录点是否被访问过
void DFS(MGraph g, int v)    		//v 表示当前所在的顶点
{
    cout << v << " ";    
    visited[v] = 1;    				//标记已访问
    for (int i = 1; i <= g.n; i++)    
    {
	if (g.edges[v][i] == 1 && visited[i] == 0) //当前顶点与 i 顶点邻接且未被访问，递归搜索
	{
	    DFS(g, i);    
	}
    }
}

BFS(广度优先)

其方法使用队列，类似与层次遍历。

int visited[MAXNUM]={0}           //定义visited数组记录点是否被访问过
void BFS(MGraph g, int v)
{
    int front, rear;    //头指针与尾指针
    int vex[MAXV];    //构造队列结构
 
    front = 0;
    vex[front] = v;    //顶点 v 入队列
    visited[v] = 1;    //标记已访问
    rear = 1;
    while (front != rear)    //队列不为空，搜索继续
    {
	for (int i = 1; i <= g.n; i++)    //遍历表头顶点的邻接点
	{
	    if (g.edges[point[front]][i] == 1 && visited[i] == 0)
	    {
	        vex[rear++] = i;    //顶点 i 入队列
		    visited[i] = 1;    //标记顶点已访问
	    }
        }
	cout << vex[front++] << " ";    
}

生成树

n个顶点有且只有(n-1)条边构成的连通无回路图。

最小生成树

边权值最小的生成树。

Prim

O(n^2),适用于稠密图

Kruskal

O(nlogn),适用于稀疏图

最短路径

Dijkstra

O(n^2)

Floyd

O(n^3)

拓扑排序

在一个有向图中找一个拓扑序列的过程。O(n+e)

具体方法：

1. 从有向图中选择一个没有前驱（即入度为0）的顶点并且输出它
2. 从图中删去该顶点，并且删去从该顶点发出的全部有向边
3. 重复上述两步，直到剩余的图中不再存在没有前驱的顶点为止

疑难问题

作者在运用Dijkstra的时候，最先搞不懂S数组的进入顺序，最后发现，其进入顺序追随Dist的变化，依次进入最小值的点。

参考资料

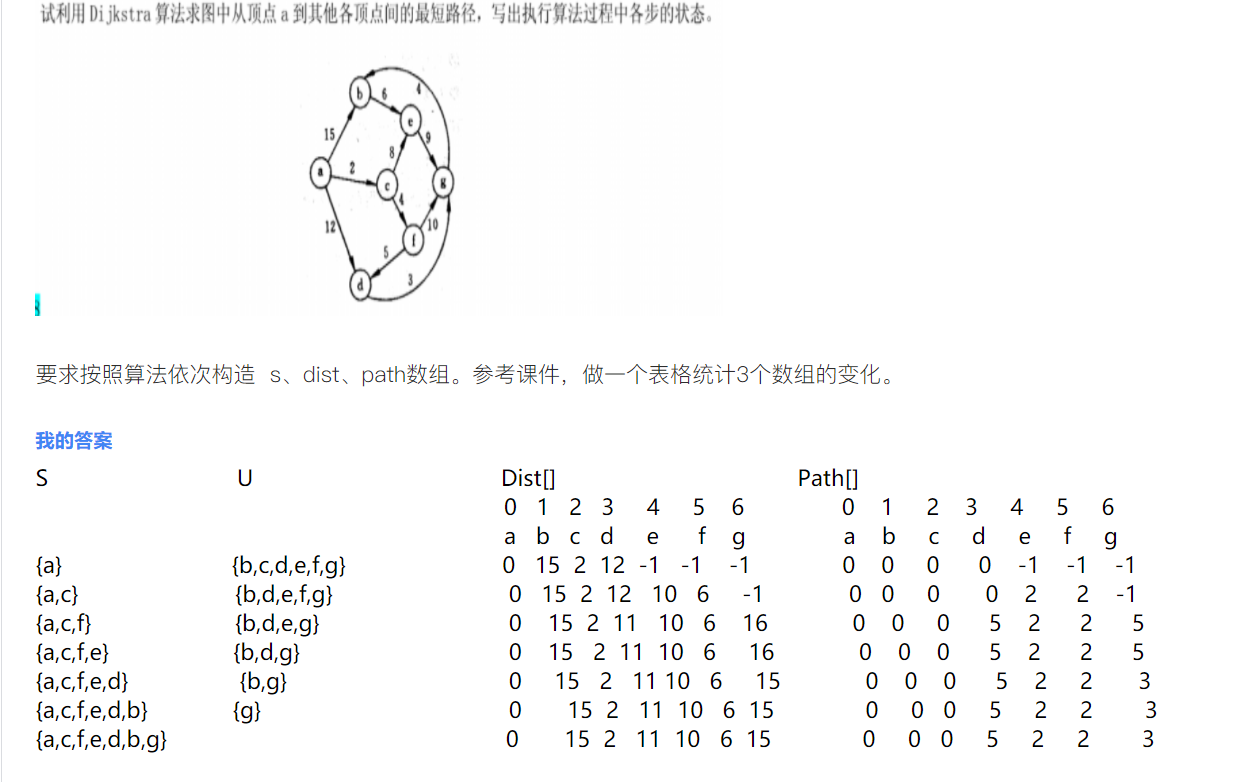
《数据结构教程（第5版）》——李春葆 主编，清华大学出版社

数据结构——图

原文：https://www.cnblogs.com/ulage/p/14829424.html