图总结

图的思维导图

疑难问题

图的遍历

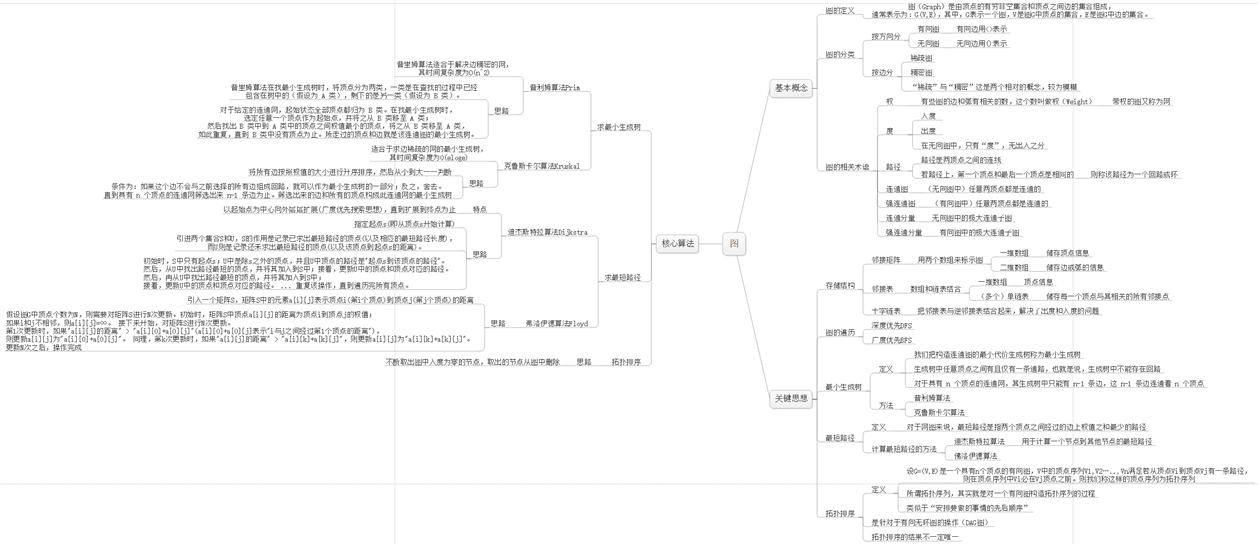
图的遍历是指，从给定图中任意指定的顶点（称为初始点）出发，按照某种搜索方法沿着图的边访问图中的所有顶点，使每个顶点仅被访问一次，这个过程称为图的遍历。遍历过程中得到的顶点序列称为图遍历序列。
图的遍历过程中，根据搜索方法的不同，又可以划分为两种搜索策略：
（1）深度优先搜索（DFS，Depth First Search）
（2）广度优先搜索（BFS，Breadth First Search）
（仅介绍无向图）

深度优先遍历

#include <stdio.h>

int e[100][100], book[100], n, sum = 0;

void dfs(int cur) {
  int i;
  printf("%d ", cur);
  sum++;
  
  // 边界
  if (sum == n) {
    return;
  }

  // 尝试每一步
  for (i = 1; i <=n; i++) {
    if (e[cur][i] == 1 && book[i] == 0) {
      book[i] = 1;
      dfs(i);
    }
  }
}

int main(void) {
  int i, j, m, a, b;

  scanf("%d %d", &n, &m);
  
  for (i = 1; i <= n; i++)
    for (j = 1; j <= n; j++)
      if (i == j) e[i][j] = 0;
        else e[i][j] = 9;

  // 二位数组是沿着主对角线对称，即无向图
  for (i = 1; i <= m; i++) {
    scanf("%d %d", &a, &b);
    e[a][b] = 1;
    e[b][a] = 1;
  }

  book[1] = 1;
  dfs(1);

  printf("\n");  

  for (i = 1; i <= n; i++) {
    for (j = 1; j <= n; j++) {
      printf("%5d ", e[i][j]);
    }
    printf("\n");
  }

  return 0;
}

广度优先遍历

#include <stdio.h>

int main(void) {
  int e[100][100], book[100] = {0}, n, sum = 0;
  int i, j, m, a, b, cur;
  
  // 初始化队列
  struct node {
    int n;
  } que[100];
  int head = 0;
  int tail = 0;

  scanf("%d %d", &n, &m);
  
  for (i = 1; i <= n; i++)
    for (j = 1; j <= n; j++)
      if (i == j) e[i][j] = 0;
        else e[i][j] = 9;

  // 二位数组是沿着主对角线对称，即无向图
  for (i = 1; i <= m; i++) {
    scanf("%d %d", &a, &b);
    e[a][b] = 1;
    e[b][a] = 1;
  }

  book[1] = 1;
  que[tail].n = 1;
  tail++;

  while (head < tail) {
    cur = que[head].n;
    
    for (i = 1; i <= n; i++) {
      if (e[cur][i] == 1 && book[i] == 0) {
        book[i] = 1;
        que[tail].n = i;
        tail++;
      }

      if (tail > n) {
        break;
      }
    }

    head++;
  }

  for (i = 0; i < tail; i++)
    printf("%d ", que[i].n);

  return 0;
}

谢谢观看

图总结

原文：https://www.cnblogs.com/sleep-early/p/m.html