递归(下)
一、全排列
把1~n这n个整数按某个顺序摆放叫这n个数的一个排列,全排列是指把这n个数所能形成的所有排列都列举出来,例如对1、2、3这个数,(1、2、3),(1、3、2),(2、1、3),(2、3、1),(3、1、2),(3、2、1)就是1、2、3的全排列。
现给出1~n,要求实现它的全排列,并且(a1,a2,a3,……an)的字典序小于(b1,b2,b3,……bn)即存在一个i,使得a1=b1,a2=b2……ai<bi成立,上面123的例子就是按字典序从小到大给出。
利用递归思想,就需要把这个问题分割为数个小问题,可以尝试把问题分割成,输入1开头的全排列,输出2开头的全排列,……输出n开头的全排列。设一个数组P存放当前排列;再设定一个散列数组hashTable,其中hashTable[x]记录了整数x是否在数组P中。
可以假设P[1]~P[index-1]已经填好了数字,现在需要从hashTable中找出第一个不为true的元素的下标,这个下标对应的整数就不在P中,且这个整数是最小的那个整数,就满足字典序从小到大给出的要求
下面给出代码

二、n皇后问题
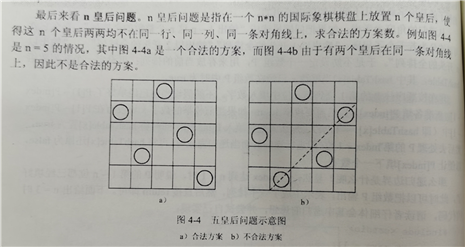
考虑每行每列只能放一个皇后,就可以把n列皇后的行号写出,就是1~n的排列算法,如图a中第一列皇后所占为第二行,那么就是n=1时P[n]=2,所以可以枚举出所有可能的排列,然后判断是否处于同一条对角线,把处在同一对角线的情况去除,就可以得出所有的合法排列。所以对于上面的全排列算法,可以在递归边界添加一些条件,判断排列的合法性。
接下来考虑合法性问题,如果两个元素处在同一条对角线上那么这两个元素必定是正方形的两个角,可以参考图(b),不合法元素处在一个正方形的两个角上,那么可以得到当两个元素行号的差值与列号的差值相同时(符合正方形四边相等条件),那么这两个元素位置就是不合法的。
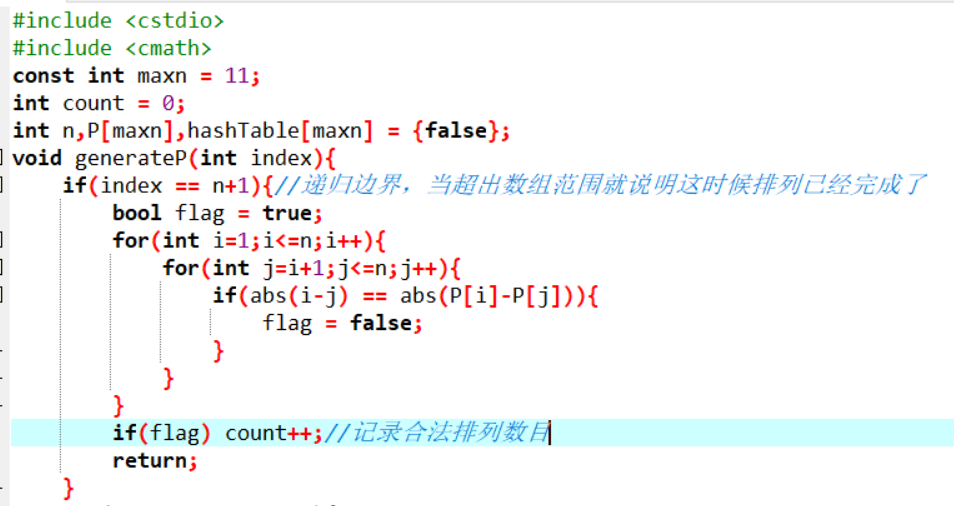
只需要对递归边界进行修改就可以实现该算法。
下面对递归算法进行一些优化,其实完全没有必要在所有元素的排列得出后再对合法性进行检查,我们可以在每次添加一个元素后就进行一次合法性检查,所以可以在递归边界和递归函数入口之间加一个合法性判断,如果不合法那么此次递归直接结束,直接开始计算下一个排列;


原文:https://www.cnblogs.com/zyq79434/p/14823993.html