一、回顾

生成树

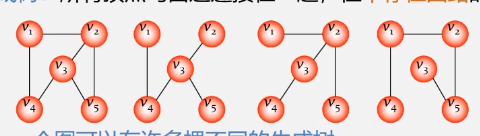
1. 所有顶点均由边连接，且不连接

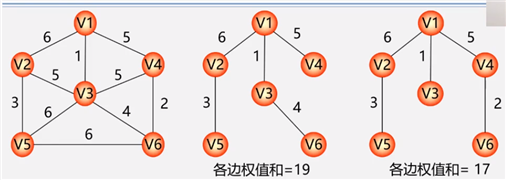
2. 所有生成树具有以下不同热点:

   • 生成树的顶点个数与图的顶点个数相同
   • 生成树是图的极小连通子图，去掉一条边则非连通
   • 生成树任意两点间的路径是唯一的
   • 一个有n个顶点的连通图的生成树有n-1条边
   • 生成树中再加一条边必形成回路

3. 含有n个顶点n-1条边的图不一定是生成树

无向图的生成树

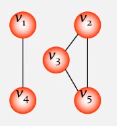
利用图的深度优先遍历生成-->深度优先生成树

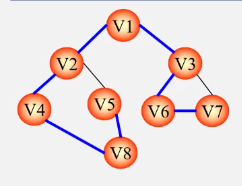
利用图的广度优先遍历生成-->广度优先生成树

构造生成树思路：顶 点用边连起来，还不能出现回路。

构造生成树原则：

• 必须只是用该网中的边来构造
• 必须使用且仅使用n-1条边连结网络总的n个顶点
• 不能产生回路的边

二、最小生成树

定义：给定一个无向网络，该网的所有生成树中，使各边权值之和最小的那棵生成树称该网的最小生成树，也叫最小代价生成树

求最小生成树

• 使用不能遍历图的方法，可以得到不同的生成树
• 从不同顶点出发，可以得到不同的生成树
• MST性质（Minimum Spanning Tree）
  • 设N = （V,E）是一个联通网，U是顶点集V的一个非空子集。若边（u，v）是一条具有最小权值的边，其中u∈U，v∈V-U，则必存在一棵包含边（u，v）的最小生成树
    
  • MST性质解释
    • 生成树构造过程中，图中n个顶点属于两个集合：
      1. 已落在生成树上的顶点集:U
      2. 尚未落在生成树上的顶点集:V-U
    • 在所有连通U中顶点和V-U中顶点的边中选权值最小的边
      

构造最小生成树方法一：普力姆算法（Prim）

算法思想：

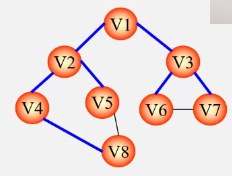
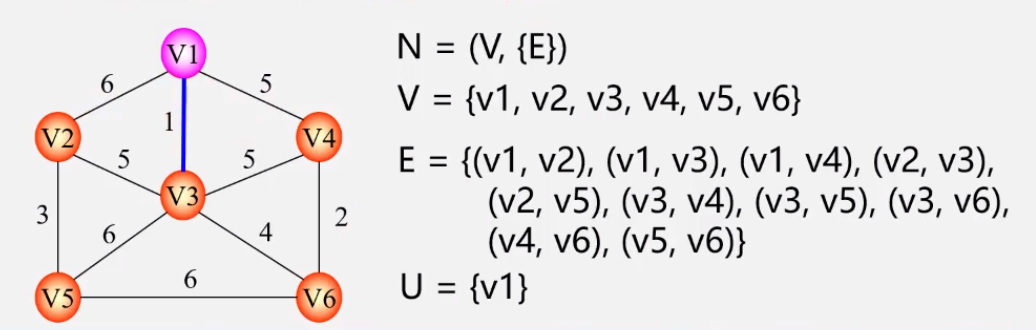
* 设N = （V,E）一个连通网，TE是N上最小生成树的**边的集合**         解释：有一个连通网，TE是最小生成树
* 初始化令U={uo}，（uo∈V，）TE={}                               解释：初始化：TE没有边，U也没有最小生成树的顶点集合
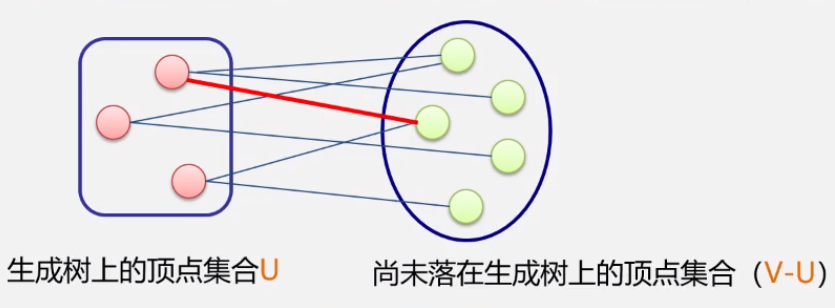
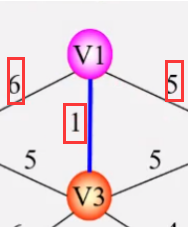
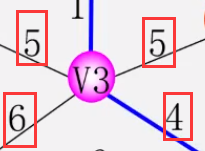
* 在所有u∈U，v∈V-U的边（u，v）∈E中，找一条代价最小的边（uo，vo） 解释：在所有顶点中随意找一个顶点，此顶点属于并入最小生成树的顶点。然后在与非并入TE的顶点中找一条**代价最小的边**
* 将（uo，vo）并入集合TE，同时vo并于U                             解释：将代价最小边并入最小生成树
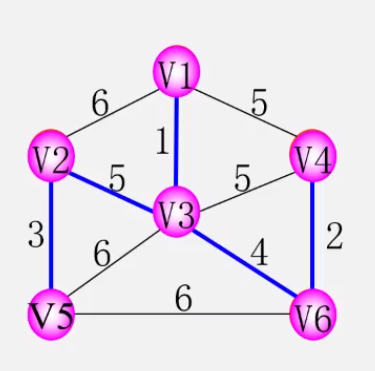
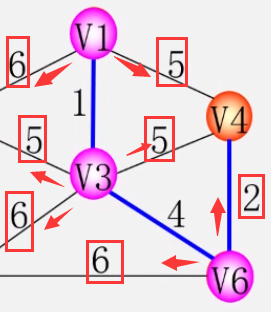
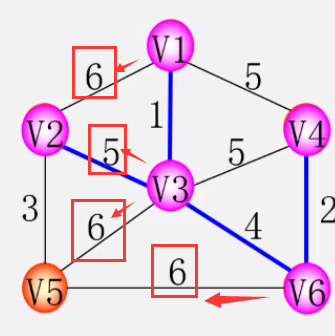
* 重复上述操作，直到U=V为止，则T=(V,TE)为N的最小生成树             解释：在并入最小生成树中的顶点中，找连接非并入最小生成树顶点的代价最小边，然后重复

• 第一步：
• 第二步：
• 第三步：
• 第四步：
• 第五步：

构造最小生成树方法一：克鲁斯卡尔算法（Kruskal）

算法思想：

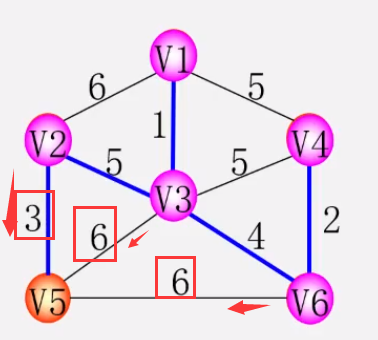
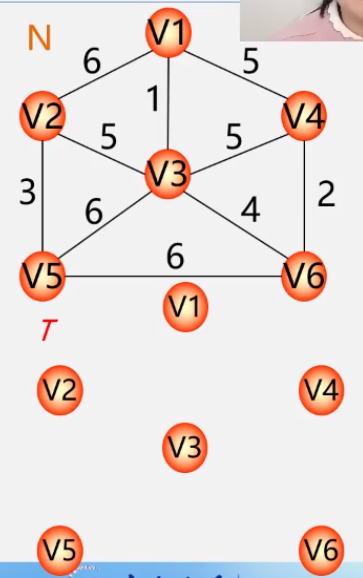
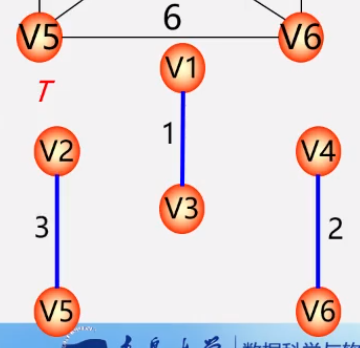
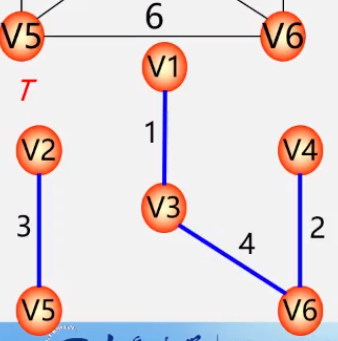
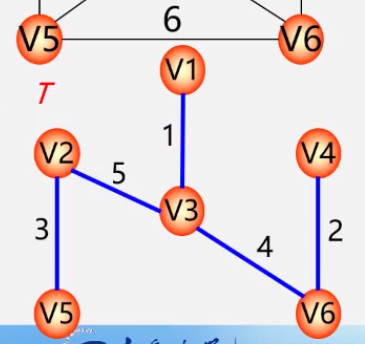
* 设N = （V,E）一个连通网，令最小生成树初始状态为**只有n个顶点而无边**的非连通图T=（V,{}）,每个顶点自成一个连通分量。
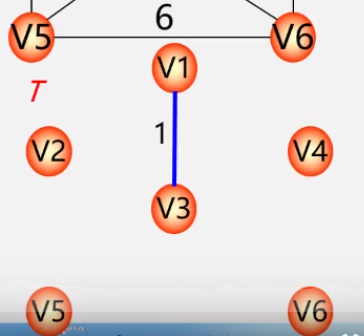
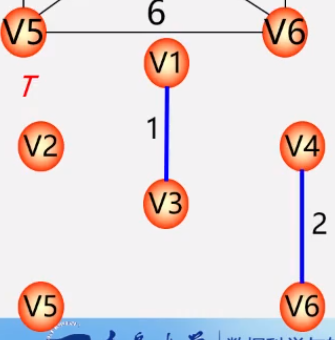
* 在E中选取代价最小的边，该边依附的顶点落在T中不同连通分量上**（不能成为环）**，则将此边加入T中，否则，舍去此边。
* 依次类推，直至T中所有顶顶啊都在同一连通分量上为止。

• 第一步：
• 第二步：
• 第三步：
• 第四步：
• 第五步：
• 第六步：

注意：最小生成树可能不唯一

两种算法比较：

数据结构与算法基础之图的应用-最小生成树

原文：https://www.cnblogs.com/lj15941314/p/14800705.html